
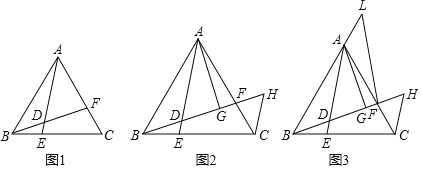
【题目】![]() 中,
中,![]() ,
,![]() 的顶点
的顶点![]() 是底边
是底边![]() 的中点,两边分别与
的中点,两边分别与![]() 交于点
交于点![]() .
.
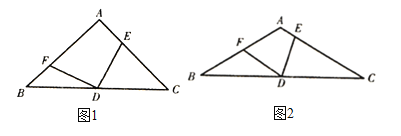
(1)如图1,![]() ,当
,当![]() 的位置变化时,
的位置变化时,![]() 是否随之变化?证明你的结论;
是否随之变化?证明你的结论;
(2)如图2,当![]() ,当
,当![]() °时,(1)中的结论仍然成立,求出此时
°时,(1)中的结论仍然成立,求出此时![]() 的值.
的值.
【答案】(1)BF+CE=a,是定值,不变.见解析;(2)60,9
【解析】
(1)结论:BF+CE=a,是定值.如图1中,连接AD.只要证明△BDF≌△ADE即可解决问题;
(2)当∠EDF=60°时,BF+EC=9,是定值.连接AD,作DM⊥AB于M,DN⊥AC于N.只要证明△DMF≌△DNE(ASA),推出FM=EN,由含30°的直角三角形的性质,推出BM=CN=![]() ,推出BF+CE=BMFM+CN+EN=2BM,即可解决问题.
,推出BF+CE=BMFM+CN+EN=2BM,即可解决问题.
解:(1)结论:BF+CE=a,是定值.
理由:如图1中,连接AD.
∵AB=AC,∠BAC=90°,BD=CD,
∴AD⊥BC,∠B=∠C=∠BAD=∠CAD=45°,AD=BD=CD.
∵∠EDF=∠ADB=90°,
∴∠BDF=∠ADE,
∴△BDF≌△ADE(ASA),
∴BF=AE,
∴BF+CE=AE+CE=AC=a,是定值.
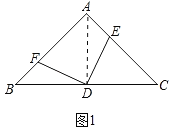
(2)当∠EDF=60°时,BF+EC=9,是定值.
理由:如图2中,连接AD,作DM⊥AB于M,DN⊥AC于N.
∵∠AMD=∠AND=90°,∠A=120°,
∴∠MDN=∠EDF=60°,
∴∠MDF=∠NDE,
∵AB=AC,BD=CD,
∴∠BAD=∠CAD,
∵DM⊥AB于M,DN⊥AC于N,
∴DM=DN,
∴△DMF≌△DNE(ASA),
∴FM=EN,
∵AB=AC,BD=CD,
∴AD⊥BC.
∵∠B=∠C=30°,
∴AD=![]() AB=
AB=![]() AC=3,∠BAD=∠CAD=60°.
AC=3,∠BAD=∠CAD=60°.
又∵DM⊥AB,DN⊥AC,
∴∠ADM=∠ADN=30°,
∴AM=AN=![]() AD=
AD=![]() ,
,
∴BM=CN=![]() ,
,
∴BF+CE=BM﹣FM+CN+EN=2BM=9,是定值.


科目:初中数学 来源: 题型:
【题目】某文化用品商店用![]() 元采购一批书包,上市后发现供不应求,很快销售完了.商店又去采购第二批同样款式的书包,进货单价比第一次高
元采购一批书包,上市后发现供不应求,很快销售完了.商店又去采购第二批同样款式的书包,进货单价比第一次高![]() 元,商店用了
元,商店用了![]() 元,所购数量是第一次的
元,所购数量是第一次的![]() 倍.
倍.
(1)求第一批采购的书包的单价是多少元?
(2)若商店按售价为每个书包![]() 元,销售完这两批书包,总共获利多少元?
元,销售完这两批书包,总共获利多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(数学问题)在同一直角坐标系内直线![]() 与
与![]() ,当
,当![]() 满足什么条件时,这两条直线互相垂直?
满足什么条件时,这两条直线互相垂直?
探究问题:我们采取一般问题特殊化的策略来进行探究.
探究一:如图①,在同一直角坐标系内直线![]() 与
与![]() 有怎样的位置关系?
有怎样的位置关系?
解:如图①,设点![]() 在直线
在直线![]() 上,则点
上,则点![]() 一定在直线
一定在直线![]() 上.过点
上.过点![]() 分别作
分别作![]() 的垂线,垂足分别为
的垂线,垂足分别为![]() .
.
则![]() ,
,![]()
∴![]()
∵![]()
∴![]()
所以,在同一直角坐标系内直线![]() 与
与![]() 互相垂直.
互相垂直.
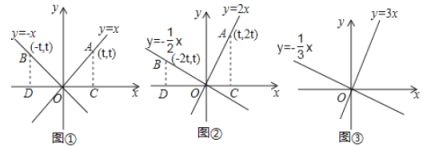
探究二:如图②,在同一直角坐标系内直线![]() 上,则点
上,则点![]() 一定在直线
一定在直线![]() 上.过点
上.过点![]() 分别作
分别作![]() 轴的垂线,垂足分别为
轴的垂线,垂足分别为![]() .
.
∵![]() ,
,![]() ,
,![]() ,
,![]()
∴![]() ,
,![]()
又∵![]()
∴![]()
∴![]()
又∵![]()
∴![]()
∵![]()
∴![]()
所以,在同一直角坐标系内直线![]() 与
与![]() 互相垂直.
互相垂直.
探究三:如图③,在同一直角坐标系内直线![]() 与
与![]() 有怎样的位置关系?
有怎样的位置关系?
(仿照上述方法解答,写出探究过程)
(1)在同一直角坐标系内直线![]() 与
与![]() ,当
,当![]() 满足数量关系为 时,这两条直线互相垂直.
满足数量关系为 时,这两条直线互相垂直.
(2)在同一直角坐标系内已知直线![]() 与直线
与直线![]() ,使它与直线
,使它与直线![]() 互相垂直,
互相垂直,![]() 的值为: ;两直线垂足的坐标为: .
的值为: ;两直线垂足的坐标为: .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商场销售某种品牌的手机,每部进货价为2500元.市场调研表明:当销售价为2900元时,平均每天能售出8部;而当销售价每降低50元时,平均每天就能多售出4部.
(1)当售价为2800元时,这种手机平均每天的销售利润达到多少元?
(2)若设每部手机降低x元,每天的销售利润为y元,试写出y与x之间的函数关系式.
(3)商场要想获得最大利润,每部手机的售价应订为为多少元?此时的最大利润是多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
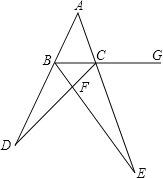
【题目】△ABC是等边三角形,点E、F分别是边BC、AC上的点,且BE=CF,AE、BF交于点D.
(1)如图1,求证:AE=BF.
(2)如图2,过点A作AG⊥BF于点G,过点C作CH∥AE交BF延长线于点H,若D为BG中点,求BH:CH的值;
(3)如图3,在(2)的条件下,L为BA延长线上一点,且FL=FB,△FLA的面积为2,求△ABC的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某测量队在山脚A处测得山上树顶仰角为45°(如图),测量队在山坡上前进600米到D处,再测得树顶的仰角为60°,已知这段山坡的坡角为30°,如果树高为15米,则山高为( )(精确到1米, ![]() =1.732).
=1.732).
A. 585米 B. 1014米 C. 805米 D. 820米
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在![]() 中,
中,![]() 平分
平分![]() 交
交![]() 于点
于点![]() ,延长
,延长![]() 至点
至点![]() 平分
平分![]() ,且
,且![]() 的延长线交于点
的延长线交于点![]() ,若
,若![]() .
.
![]() 求证:
求证:![]() ;
;
![]() 求
求![]() 的度数;
的度数;
![]() 若在图中继续作
若在图中继续作![]() 与
与![]() 的平分线交于点
的平分线交于点![]() ,作
,作![]() 与
与![]() 的平分线交于点
的平分线交于点![]() ,作
,作![]() 与
与![]() 的平分线交于点
的平分线交于点![]() ,以此类推,作
,以此类推,作![]() 与
与![]() 的平分线交于点
的平分线交于点![]() ,请用含有
,请用含有![]() 的式了表示
的式了表示![]() 的度数(直接写答案).
的度数(直接写答案).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小明在学习二次根式后,发现一些含根号的式子可以写成另一个式子的平方,如:3+2![]() ,善于思考的小明进行了以下探索:
,善于思考的小明进行了以下探索:
设a+b![]() (其中a、b、m、n均为整数),
(其中a、b、m、n均为整数),
则有:a+b![]() ,∴a=m2+2n2,b=2mn,这样小明就找到了一种把类似a+b
,∴a=m2+2n2,b=2mn,这样小明就找到了一种把类似a+b![]() 的式子化为平方式的方法.
的式子化为平方式的方法.
请你仿照小明的方法探索并解决下列问题:
(1)当a、b、m、n均为正整数时,若a+b![]() ,用含m、n的式子分别表示a、b得:a= ,b= ;
,用含m、n的式子分别表示a、b得:a= ,b= ;
(2)利用所探索的结论,用完全平方式表示出:7+4![]() = .
= .
(3)请化简:![]() .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com