
【题目】(数学问题)在同一直角坐标系内直线![]() 与
与![]() ,当
,当![]() 满足什么条件时,这两条直线互相垂直?
满足什么条件时,这两条直线互相垂直?
探究问题:我们采取一般问题特殊化的策略来进行探究.
探究一:如图①,在同一直角坐标系内直线![]() 与
与![]() 有怎样的位置关系?
有怎样的位置关系?
解:如图①,设点![]() 在直线
在直线![]() 上,则点
上,则点![]() 一定在直线
一定在直线![]() 上.过点
上.过点![]() 分别作
分别作![]() 的垂线,垂足分别为
的垂线,垂足分别为![]() .
.
则![]() ,
,![]()
∴![]()
∵![]()
∴![]()
所以,在同一直角坐标系内直线![]() 与
与![]() 互相垂直.
互相垂直.
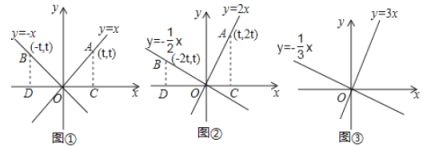
探究二:如图②,在同一直角坐标系内直线![]() 上,则点
上,则点![]() 一定在直线
一定在直线![]() 上.过点
上.过点![]() 分别作
分别作![]() 轴的垂线,垂足分别为
轴的垂线,垂足分别为![]() .
.
∵![]() ,
,![]() ,
,![]() ,
,![]()
∴![]() ,
,![]()
又∵![]()
∴![]()
∴![]()
又∵![]()
∴![]()
∵![]()
∴![]()
所以,在同一直角坐标系内直线![]() 与
与![]() 互相垂直.
互相垂直.
探究三:如图③,在同一直角坐标系内直线![]() 与
与![]() 有怎样的位置关系?
有怎样的位置关系?
(仿照上述方法解答,写出探究过程)
(1)在同一直角坐标系内直线![]() 与
与![]() ,当
,当![]() 满足数量关系为 时,这两条直线互相垂直.
满足数量关系为 时,这两条直线互相垂直.
(2)在同一直角坐标系内已知直线![]() 与直线
与直线![]() ,使它与直线
,使它与直线![]() 互相垂直,
互相垂直,![]() 的值为: ;两直线垂足的坐标为: .
的值为: ;两直线垂足的坐标为: .
【答案】探究三:互相垂直,详见解析;(1)![]() ;(2)k= -5,(2,0.4)
;(2)k= -5,(2,0.4)
【解析】
探究三:仿照探究一与探究二,在两直线![]() 与
与![]() 上取点,证明三角形全等,由此得到结论;
上取点,证明三角形全等,由此得到结论;
(1)由探究即可得到答案;
(2)利用前面的结论得到k的值,再解两直线解析式组成的方程组即可得到答案.
探究三:在同一直角坐标系内直线![]() 与
与![]() 互相垂直,
互相垂直,
如图,设点A(a,3a)在直线y=3x上,则点B(-3a,a)在直线![]() 上,
上,
作AC⊥x轴,BD⊥x轴,
∵OC=a,AC=3a,OD=3a,BD=a,
∴![]() ,
,![]() ,
,
又∵![]() ,
,
∴△AOC≌△OBD,
∴![]() ,
,
又∵![]() ,
,
∴![]() ,
,
∵![]() ,
,
∴![]()
∴在同一直角坐标系内直线![]() 与
与![]() 互相垂直
互相垂直
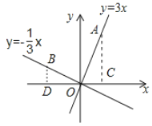
(1)由探究一、二、三可知,当两条直线在同一平面内互相垂直时,两条直线的k值互为负倒数,
∴在同一直角坐标系内直线![]() 与
与![]() ,当这两条直线互相垂直时,
,当这两条直线互相垂直时,![]() ,
,
故答案为:![]() ;
;
(2)∵直线![]() 与直线
与直线![]() 互相垂直,
互相垂直,
∴0.2k=-1,
∴k=-5,
∴该直线的解析式为y=-5x+10.4,
解方程组![]() ,得
,得![]() ,
,
∴两直线垂足的坐标为(2,0.4),
故答案为:k=-5,(2,0.4).


 千里马走向假期期末仿真试卷寒假系列答案
千里马走向假期期末仿真试卷寒假系列答案科目:初中数学 来源: 题型:
【题目】如图,三角形纸片中,AB=5cm,AC=7cm,BC=9cm.沿过点B的直线折叠这个三角形,使点A落在BC边上的点E处,折痕为BD,则△DEC的周长是________cm.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某服装店用4500元购进A,B两种新式服装,按标价售出后可获得毛利润2800元(毛利润=售价一进价),这两种服装的进价、标价如表所示
类型价格 | A型 | B型 |
进价(元/件) | 60 | 100 |
标价(元/件) | 100 | 160 |
(1)请利用二元一次方程组求A,B两种新式服装各购进的件数;
(2)如果A种服装按标价的9折出售,B种服装按标价的8折出售,那么这批服装全部售完后,服装店比按标价出售少收入多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
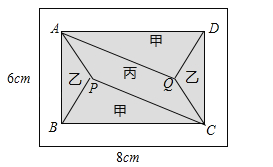
【题目】(2017浙江省温州市)小黄准备给长8m,宽6m的长方形客厅铺设瓷砖,现将其划分成一个长方形ABCD区域Ⅰ(阴影部分)和一个环形区域Ⅱ(空白部分),其中区域Ⅰ用甲、乙、丙三种瓷砖铺设,且满足PQ∥AD,如图所示.
(1)若区域Ⅰ的三种瓷砖均价为300元/m2,面积为S(m2),区域Ⅱ的瓷砖均价为200元/m2,且两区域的瓷砖总价为不超过12000元,求S的最大值;
(2)若区域Ⅰ满足BC=2:3,区域Ⅱ四周宽度相等.
①求AB,BC的长;
②若甲、丙两瓷砖单价之和为300元/m2,乙、丙瓷砖单价之比为5:3,且区域Ⅰ的三种瓷砖总价为4800元,求丙瓷砖单价的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校的一个数学兴趣小组在本校学生中开展主题为“环广西公路自行车世界巡回赛”的专题调查活动,取随机抽样的方式进行问卷调查,问卷调查的结果分为“非常了解”、“比较了解”、“基本了解”、“不太了解”四个等级,分别记作A、B、C、D;并根据调查结果绘制成如图所示不完整的统计图,请结合图中信息解答下列问题:

(1)请求出本次被调查的学生共多少人,并将条形统计图补充完整.
(2)估计该校1500名学生中“C等级”的学生有多少人?
(3)在“B等级”的学生中,初三学生共有4人,其中1男3女,在这4个人中,随机选出2人进行采访,则所选两位同学中有男同学的概率是多少?请用列表法或树状图的方法求解.
查看答案和解析>>
科目:初中数学 来源: 题型:
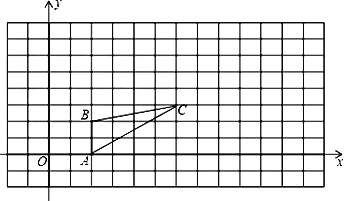
【题目】如图,图中的小方格都是边长为1的正方形,△ABC的A、B、C三点坐标为A(2,0)、B(2,2)、C(6,3)。
(1) 请在图中画出一个△![]() ,使△
,使△![]() 与△ABC是以坐标原点为位似中心,相似比为2的位似图形。
与△ABC是以坐标原点为位似中心,相似比为2的位似图形。
(2)求△![]() 的面积。
的面积。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,以正方形的中心O为顶点作一个直角,直角的两边分别交正方形的两边BC、DC于E、F点,问:
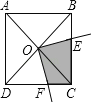
(1)△BOE与△COF有什么关系?证明你的结论(提示:正方形的对角线把正方形分成全等的四个等腰直角三角形,即正方形的对角线垂直相等且相互平分);
(2)若正方形的边长为2,四边形EOFC的面积为多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】![]() 中,
中,![]() ,
,![]() 的顶点
的顶点![]() 是底边
是底边![]() 的中点,两边分别与
的中点,两边分别与![]() 交于点
交于点![]() .
.
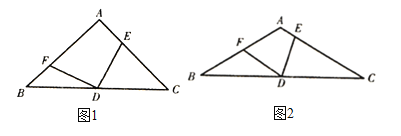
(1)如图1,![]() ,当
,当![]() 的位置变化时,
的位置变化时,![]() 是否随之变化?证明你的结论;
是否随之变化?证明你的结论;
(2)如图2,当![]() ,当
,当![]() °时,(1)中的结论仍然成立,求出此时
°时,(1)中的结论仍然成立,求出此时![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商店用1000元人民币购进某种水果销售,过了一周时间,又用 2 400元人民币购进这种水果,所购数量是第一次购进数量的2倍,但每千克的价格比第一次购进的价格贵了2元.
(1)该商店第一次购进这种水果多少千克?
(2)假设该商店两次购进的这种水果按相同的标价销售,最后剩下的20千克按标价的五折优惠销售.若两次购进的这种水果全部售完,利润不低于950元,则每千克这种水果的标价至少是多少元?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com