
【题目】某商店用1000元人民币购进某种水果销售,过了一周时间,又用 2 400元人民币购进这种水果,所购数量是第一次购进数量的2倍,但每千克的价格比第一次购进的价格贵了2元.
(1)该商店第一次购进这种水果多少千克?
(2)假设该商店两次购进的这种水果按相同的标价销售,最后剩下的20千克按标价的五折优惠销售.若两次购进的这种水果全部售完,利润不低于950元,则每千克这种水果的标价至少是多少元?
【答案】(1)该商店第一次购进水果100千克;(2)每千克这种水果的标价至少是15元.
【解析】
(1)设该商店第一次购进水果x千克,则第二次购进水果2x千克,然后根据每千克的价格比第一次购进的价格贵了2元,列出方程求解即可;
(2)设每千克水果的标价是y元,然后根据两次购进水果全部售完,利润不低于950元列出不等式,然后求解即可得出答案.
(1)设该商店第一次购进水果x千克,则第二次购进这种水果2x千克.
由题意,得![]() ,
,
解得x=100.
经检验,x=100是所列方程的解.
答:该商店第一次购进水果100千克.
(2)设每千克这种水果的标价是 y 元,则
(100+100×2﹣20)y+20×0.5 y≥1000+2400+950,
解得y≥15.
答:每千克这种水果的标价至少是15元.


科目:初中数学 来源: 题型:
【题目】(数学问题)在同一直角坐标系内直线![]() 与
与![]() ,当
,当![]() 满足什么条件时,这两条直线互相垂直?
满足什么条件时,这两条直线互相垂直?
探究问题:我们采取一般问题特殊化的策略来进行探究.
探究一:如图①,在同一直角坐标系内直线![]() 与
与![]() 有怎样的位置关系?
有怎样的位置关系?
解:如图①,设点![]() 在直线
在直线![]() 上,则点
上,则点![]() 一定在直线
一定在直线![]() 上.过点
上.过点![]() 分别作
分别作![]() 的垂线,垂足分别为
的垂线,垂足分别为![]() .
.
则![]() ,
,![]()
∴![]()
∵![]()
∴![]()
所以,在同一直角坐标系内直线![]() 与
与![]() 互相垂直.
互相垂直.
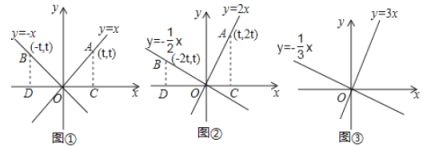
探究二:如图②,在同一直角坐标系内直线![]() 上,则点
上,则点![]() 一定在直线
一定在直线![]() 上.过点
上.过点![]() 分别作
分别作![]() 轴的垂线,垂足分别为
轴的垂线,垂足分别为![]() .
.
∵![]() ,
,![]() ,
,![]() ,
,![]()
∴![]() ,
,![]()
又∵![]()
∴![]()
∴![]()
又∵![]()
∴![]()
∵![]()
∴![]()
所以,在同一直角坐标系内直线![]() 与
与![]() 互相垂直.
互相垂直.
探究三:如图③,在同一直角坐标系内直线![]() 与
与![]() 有怎样的位置关系?
有怎样的位置关系?
(仿照上述方法解答,写出探究过程)
(1)在同一直角坐标系内直线![]() 与
与![]() ,当
,当![]() 满足数量关系为 时,这两条直线互相垂直.
满足数量关系为 时,这两条直线互相垂直.
(2)在同一直角坐标系内已知直线![]() 与直线
与直线![]() ,使它与直线
,使它与直线![]() 互相垂直,
互相垂直,![]() 的值为: ;两直线垂足的坐标为: .
的值为: ;两直线垂足的坐标为: .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某测量队在山脚A处测得山上树顶仰角为45°(如图),测量队在山坡上前进600米到D处,再测得树顶的仰角为60°,已知这段山坡的坡角为30°,如果树高为15米,则山高为( )(精确到1米, ![]() =1.732).
=1.732).
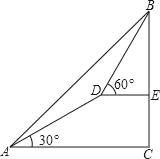
A. 585米 B. 1014米 C. 805米 D. 820米
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在![]() 中,
中,![]() 平分
平分![]() 交
交![]() 于点
于点![]() ,延长
,延长![]() 至点
至点![]() 平分
平分![]() ,且
,且![]() 的延长线交于点
的延长线交于点![]() ,若
,若![]() .
.
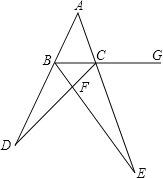
![]() 求证:
求证:![]() ;
;
![]() 求
求![]() 的度数;
的度数;
![]() 若在图中继续作
若在图中继续作![]() 与
与![]() 的平分线交于点
的平分线交于点![]() ,作
,作![]() 与
与![]() 的平分线交于点
的平分线交于点![]() ,作
,作![]() 与
与![]() 的平分线交于点
的平分线交于点![]() ,以此类推,作
,以此类推,作![]() 与
与![]() 的平分线交于点
的平分线交于点![]() ,请用含有
,请用含有![]() 的式了表示
的式了表示![]() 的度数(直接写答案).
的度数(直接写答案).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】国庆期间某一位公司老板准备组织员工去上海旅游,甲旅行社承诺:“老板一人免费,员工可享受八折优惠”;乙旅行社承诺:“包括老板在内所有按全票的七五折优惠”,若全票价为2000元
(1)设员工人数为![]() ,甲、乙旅行社收费分别为
,甲、乙旅行社收费分别为![]() 甲(元)和
甲(元)和![]() 乙(元), 分别写出两个旅行社收费的表达式;
乙(元), 分别写出两个旅行社收费的表达式;
(2)当有员工10人时,哪家旅行社更优惠?
(3)当员工人数为多少时,两家旅行社收费相同?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在⊙O的内接四边形ABCD中,AB=AD,∠C=120°,点E在⊙O上.
(1)求∠AED的度数;
(2)若⊙O的半径为2,则![]() 的长为多少?
的长为多少?
(3)连接OD,OE,当∠DOE=90°时,AE恰好是⊙O的内接正n边形的一边,求n的值.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某中学“书香文化进校园”活动筹备小组准备购买![]() 两种类型的毛笔,已知购买一支
两种类型的毛笔,已知购买一支![]() 类型的毛笔比购买一支
类型的毛笔比购买一支![]() 类型的毛笔多花30元;且购买
类型的毛笔多花30元;且购买![]() 类型的毛笔80与购买
类型的毛笔80与购买![]() 类型的毛笔50支的价格相同.
类型的毛笔50支的价格相同.
(1)求![]() 两种类型毛笔的单价各是多少?
两种类型毛笔的单价各是多少?
(2)由于报名人数超过预期,筹备小组决定再次购买![]() 两种类型毛笔共50支.然而商店对商品价格进行了调整,
两种类型毛笔共50支.然而商店对商品价格进行了调整,![]() 类型毛笔售价比第一次购买时提高4元,B类型毛笔售价按第一次购买时售价的9折出售,如果此次购买
类型毛笔售价比第一次购买时提高4元,B类型毛笔售价按第一次购买时售价的9折出售,如果此次购买![]() 两种类型毛笔的总费用不超过3150元且保证这次购买的
两种类型毛笔的总费用不超过3150元且保证这次购买的![]() 种类型毛笔不少于23支,则这次购买方案有哪几种?
种类型毛笔不少于23支,则这次购买方案有哪几种?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小明在学习二次根式后,发现一些含根号的式子可以写成另一个式子的平方,如:3+2![]() ,善于思考的小明进行了以下探索:
,善于思考的小明进行了以下探索:
设a+b![]() (其中a、b、m、n均为整数),
(其中a、b、m、n均为整数),
则有:a+b![]() ,∴a=m2+2n2,b=2mn,这样小明就找到了一种把类似a+b
,∴a=m2+2n2,b=2mn,这样小明就找到了一种把类似a+b![]() 的式子化为平方式的方法.
的式子化为平方式的方法.
请你仿照小明的方法探索并解决下列问题:
(1)当a、b、m、n均为正整数时,若a+b![]() ,用含m、n的式子分别表示a、b得:a= ,b= ;
,用含m、n的式子分别表示a、b得:a= ,b= ;
(2)利用所探索的结论,用完全平方式表示出:7+4![]() = .
= .
(3)请化简:![]() .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com