
【题目】如图,在△ABC中,AB=AC=13,BC=10,点D为BC的中点,DE⊥AB于点E,则tan ∠BDE=

A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
科目:初中数学 来源: 题型:
【题目】九年级学生到距离学校6千米的百花公园去春游,一部分学生步行前往,20分钟后另一部分学生骑自行车前往,设![]() (分钟)为步行前往的学生离开学校所走的时间,步行学生走的路程为
(分钟)为步行前往的学生离开学校所走的时间,步行学生走的路程为![]() 千米,骑自行车学生骑行的路程为
千米,骑自行车学生骑行的路程为![]() 千米,
千米,![]() 关于
关于![]() 的函数图象如图所示.
的函数图象如图所示.
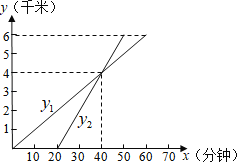
(1)求![]() 关于
关于![]() 的函数解析式;
的函数解析式;
(2)步行的学生和骑自行车的学生谁先到达百花公园,先到了几分钟?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商场销售某种品牌的手机,每部进货价为2500元.市场调研表明:当销售价为2900元时,平均每天能售出8部;而当销售价每降低50元时,平均每天就能多售出4部.
(1)当售价为2800元时,这种手机平均每天的销售利润达到多少元?
(2)若设每部手机降低x元,每天的销售利润为y元,试写出y与x之间的函数关系式.
(3)商场要想获得最大利润,每部手机的售价应订为为多少元?此时的最大利润是多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】△ABC是等边三角形,点E、F分别是边BC、AC上的点,且BE=CF,AE、BF交于点D.
(1)如图1,求证:AE=BF.
(2)如图2,过点A作AG⊥BF于点G,过点C作CH∥AE交BF延长线于点H,若D为BG中点,求BH:CH的值;
(3)如图3,在(2)的条件下,L为BA延长线上一点,且FL=FB,△FLA的面积为2,求△ABC的面积.
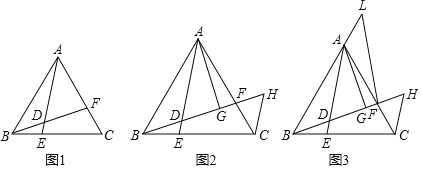
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某测量队在山脚A处测得山上树顶仰角为45°(如图),测量队在山坡上前进600米到D处,再测得树顶的仰角为60°,已知这段山坡的坡角为30°,如果树高为15米,则山高为( )(精确到1米, ![]() =1.732).
=1.732).
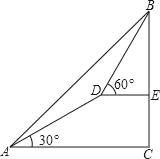
A. 585米 B. 1014米 C. 805米 D. 820米
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,某幢大楼顶部有广告牌CD,小宇身高MA为1.89米,他站在立在离大楼45米的A处测得大楼顶端点D的仰角为30°;接着他向大楼前进15米,站在点B处测得广告牌顶端点C的仰角为45°.
(1)求这幢大楼的高DH;
(2)求这块广告牌CD的高度.(取![]() ≈1.732,计算结果保留一位小数)
≈1.732,计算结果保留一位小数)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在![]() 中,
中,![]() 平分
平分![]() 交
交![]() 于点
于点![]() ,延长
,延长![]() 至点
至点![]() 平分
平分![]() ,且
,且![]() 的延长线交于点
的延长线交于点![]() ,若
,若![]() .
.
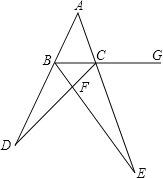
![]() 求证:
求证:![]() ;
;
![]() 求
求![]() 的度数;
的度数;
![]() 若在图中继续作
若在图中继续作![]() 与
与![]() 的平分线交于点
的平分线交于点![]() ,作
,作![]() 与
与![]() 的平分线交于点
的平分线交于点![]() ,作
,作![]() 与
与![]() 的平分线交于点
的平分线交于点![]() ,以此类推,作
,以此类推,作![]() 与
与![]() 的平分线交于点
的平分线交于点![]() ,请用含有
,请用含有![]() 的式了表示
的式了表示![]() 的度数(直接写答案).
的度数(直接写答案).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在⊙O的内接四边形ABCD中,AB=AD,∠C=120°,点E在⊙O上.
(1)求∠AED的度数;
(2)若⊙O的半径为2,则![]() 的长为多少?
的长为多少?
(3)连接OD,OE,当∠DOE=90°时,AE恰好是⊙O的内接正n边形的一边,求n的值.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com