
【题目】如图,某幢大楼顶部有广告牌CD,小宇身高MA为1.89米,他站在立在离大楼45米的A处测得大楼顶端点D的仰角为30°;接着他向大楼前进15米,站在点B处测得广告牌顶端点C的仰角为45°.
(1)求这幢大楼的高DH;
(2)求这块广告牌CD的高度.(取![]() ≈1.732,计算结果保留一位小数)
≈1.732,计算结果保留一位小数)

【答案】(1)楼高DH为27.9米;(2)广告牌CD的高度为4.0米.
【解析】
在Rt△DME与Rt△CNE;应利用ME-NE=AB=15构造方程关系式,进而可解即可求出答案.
解:(1)在Rt△DME中,ME=AH=45;由tan 30°=![]() ,得DE=45×
,得DE=45×![]() ≈15×1.732=25.98;又因为EH=MA=1.89,故大楼DH=DE+EH=25.98+1.89=27.87≈27.9.
≈15×1.732=25.98;又因为EH=MA=1.89,故大楼DH=DE+EH=25.98+1.89=27.87≈27.9.
(2)在Rt△CNE中,NE=45-15=30,由tan 45°=![]() ,得CE=NE=30,因而广告牌CD=CE-DE=30-25.98≈4.0.
,得CE=NE=30,因而广告牌CD=CE-DE=30-25.98≈4.0.
答:楼高DH为27.9米,广告牌CD的高度为4.0米.


科目:初中数学 来源: 题型:
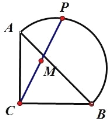
【题目】如图,在等腰 Rt△ABC 中,AC=BC=2,点 P 在以斜边 AB 为直径的半圆上,M 为 PC 的中点.当点 P 沿半圆从点A 运动至点 B 时,点 M 运动的路径长是_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
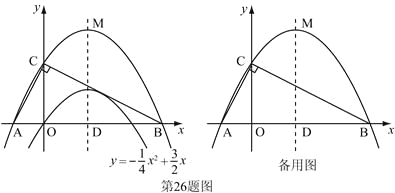
【题目】(本题满分12分)已知二次函数![]() 的图象如图.
的图象如图.
(1)求它的对称轴与![]() 轴交点D的坐标;
轴交点D的坐标;
(2)将该抛物线沿它的对称轴向上平移,设平移后的抛物线与![]() 轴,
轴,![]() 轴的交点分别为A、B、C三点,若∠ACB=90°,求此时抛物线的解析式;
轴的交点分别为A、B、C三点,若∠ACB=90°,求此时抛物线的解析式;
(3)设(2)中平移后的抛物线的顶点为M,以AB为直径,D为圆心作⊙D,试判断直线CM与⊙D的位置关系,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】计算:
(1)(2x2y)3(3x2y)
(2)(36x3-24x2+2x)÷4x
(3)(2x+y+1)(2x-y-1)
(4)(-3ax)2(5a2-3ax3)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“高低杠”是女子体操特有的一个竞技项目,其比赛器材由高、低两根平行杠及若干支架组成,运动员可根据自己的身高和习惯在规定范围内调节高、低两杠间的距离.某兴趣小组根据高低杠器材的一种截面图编制了如下数学问题,请你解答.
如图所示,底座上A,B两点间的距离为90cm.低杠上点C到直线AB的距离CE的长为155cm,高杠上点D到直线AB的距离DF的长为234cm,已知低杠的支架AC与直线AB的夹角∠CAE为82.4°,高杠的支架BD与直线AB的夹角∠DBF为80.3°.求高、低杠间的水平距离CH的长.(结果精确到1cm,参考数据sin82.4°≈0.991,cos82.4°≈0.132,tan82.4°≈7.500,sin80.3°≈0.983,cos80.3°≈0.168,tan80.3°≈5.850)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,把抛物线y=![]() x2平移得到抛物线m,抛物线m经过点A(﹣6,0)和原点O(0,0),它的顶点为P,它的对称轴与抛物线y=
x2平移得到抛物线m,抛物线m经过点A(﹣6,0)和原点O(0,0),它的顶点为P,它的对称轴与抛物线y=![]() x2交于点Q,则图中阴影部分的面积为 ▲ .
x2交于点Q,则图中阴影部分的面积为 ▲ .

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com