
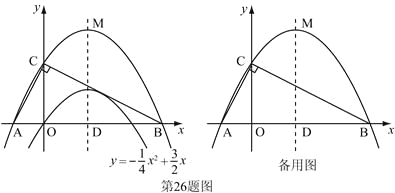
【题目】(本题满分12分)已知二次函数![]() 的图象如图.
的图象如图.
(1)求它的对称轴与![]() 轴交点D的坐标;
轴交点D的坐标;
(2)将该抛物线沿它的对称轴向上平移,设平移后的抛物线与![]() 轴,
轴,![]() 轴的交点分别为A、B、C三点,若∠ACB=90°,求此时抛物线的解析式;
轴的交点分别为A、B、C三点,若∠ACB=90°,求此时抛物线的解析式;
(3)设(2)中平移后的抛物线的顶点为M,以AB为直径,D为圆心作⊙D,试判断直线CM与⊙D的位置关系,并说明理由.
【答案】(本题满分12分)
 解: (1)由
解: (1)由![]() 得
得![]() …………1分
…………1分
∴D(3,0)…………2分
(2)方法一:
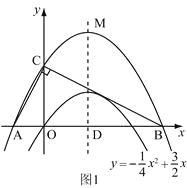
如图1, 设平移后的抛物线的解析式为
![]() …………3分
…………3分
则C![]() OC=
OC=![]()
令![]() 即
即![]()
得![]()
![]() …………4分
…………4分
∴A![]() ,B
,B![]()
∴![]() ………5分
………5分
![]()
![]() ……………………6分
……………………6分
∵![]()
即:![]()
得![]()
![]() (舍去) ……………7分
(舍去) ……………7分
∴抛物线的解析式为![]() ……………8分
……………8分
方法二:
∵![]() ∴顶点坐标
∴顶点坐标![]()
设抛物线向上平移h个单位,则得到![]() ,顶点坐标
,顶点坐标![]() …………3分
…………3分
∴平移后的抛物线:![]() ……………………4分
……………………4分
当![]() 时,
时,![]() , 得
, 得![]()
![]()
∴A![]() B
B![]() ……………………5分
……………………5分
∵∠ACB=90° ∴△AOC∽△COB
∴![]() OA·OB……………………6分
OA·OB……………………6分
![]() 得
得![]() ,
,![]() …………7分
…………7分
∴平移后的抛物线:![]() …………8分
…………8分
(3)方法一:
如图2,由抛物线的解析式![]() 可得
可得
A(-2 ,0),B(8,0),C(4,0) ,M![]() …………9分
…………9分
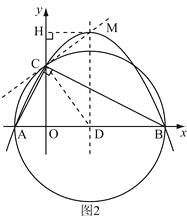 过C、M作直线,连结CD,过M作MH垂直y轴于H,
过C、M作直线,连结CD,过M作MH垂直y轴于H,
则![]()
∴![]()
![]()
在Rt△COD中,CD=![]() =AD
=AD
∴点C在⊙D上 …………………10分
∵![]()
![]() ……11分
……11分
∴![]()
∴△CDM是直角三角形,∴CD⊥CM
∴直线CM与⊙D相切 …………12分
方法二:
如图3,由抛物线的解析式可得
A(-2 ,0),B(8,0),C(4,0) ,M![]() …………9分
…………9分
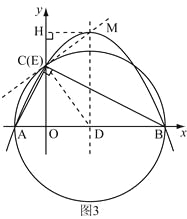 作直线CM,过D作DE⊥CM于E, 过M作MH垂直y轴于H,则
作直线CM,过D作DE⊥CM于E, 过M作MH垂直y轴于H,则![]() ,
,![]() , 由勾股定理得
, 由勾股定理得![]()
∵DM∥OC
∴∠MCH=∠EMD
∴Rt△CMH∽Rt△DME …………10分
∴![]() 得
得![]() …………11分
…………11分
由(2)知![]() ∴⊙D的半径为5
∴⊙D的半径为5
∴直线CM与⊙D相切 …………12分
【解析】
(1)根据对称轴公式求出x=﹣![]() ,求出即可;
,求出即可;
(2)假设出平移后的解析式即可得出图象与x轴的交点坐标,再利用勾股定理求出即可;
(3)由抛物线的解析式![]() 可得,A,B,C,M各点的坐标,再利用勾股定理逆定理求出CD⊥CM,即可证明.
可得,A,B,C,M各点的坐标,再利用勾股定理逆定理求出CD⊥CM,即可证明.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
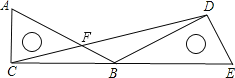
【题目】如图所示,把一个直角三角尺ACB绕着30°角的顶点B顺时针旋转,使得点A与CB的延长线上的点E重合,连接CD.
(1)试判断△CBD的形状,并说明理由;
(2)求∠BDC的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
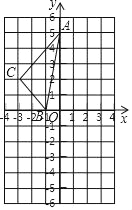
【题目】如图,在平面直角坐标系中,A(0,5)、B(﹣1,0)、C(﹣3,2).
(1)请画出将△ABC向右平移4个单位得到的△A1B1C1.
(2)请画出将△ABC关于点O成中心对称的△A2B2C2.
(3)请直接写出△A1B1C1与△A2B2C2的对称中心的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商场销售某种品牌的手机,每部进货价为2500元.市场调研表明:当销售价为2900元时,平均每天能售出8部;而当销售价每降低50元时,平均每天就能多售出4部.
(1)当售价为2800元时,这种手机平均每天的销售利润达到多少元?
(2)若设每部手机降低x元,每天的销售利润为y元,试写出y与x之间的函数关系式.
(3)商场要想获得最大利润,每部手机的售价应订为为多少元?此时的最大利润是多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知直线l:y=kx和抛物线C:y=ax2+bx+1.
(1)当k=1,b=1时,抛物线C:y=ax2+bx+1的顶点在直线l:y=kx上,求a的值;
(2)若把直线l向上平移k2+1个单位长度得到直线r,则无论非零实数k取何值,直线r与抛物线C都只有一个交点;
(i)求此抛物线的解析式;
(ii)若P是此抛物线上任一点,过点P作PQ∥y轴且与直线y=2交于点Q,O为原点,
求证:OP=PQ.
查看答案和解析>>
科目:初中数学 来源: 题型:
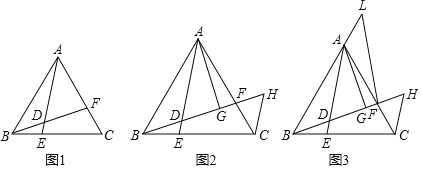
【题目】△ABC是等边三角形,点E、F分别是边BC、AC上的点,且BE=CF,AE、BF交于点D.
(1)如图1,求证:AE=BF.
(2)如图2,过点A作AG⊥BF于点G,过点C作CH∥AE交BF延长线于点H,若D为BG中点,求BH:CH的值;
(3)如图3,在(2)的条件下,L为BA延长线上一点,且FL=FB,△FLA的面积为2,求△ABC的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,某幢大楼顶部有广告牌CD,小宇身高MA为1.89米,他站在立在离大楼45米的A处测得大楼顶端点D的仰角为30°;接着他向大楼前进15米,站在点B处测得广告牌顶端点C的仰角为45°.
(1)求这幢大楼的高DH;
(2)求这块广告牌CD的高度.(取![]() ≈1.732,计算结果保留一位小数)
≈1.732,计算结果保留一位小数)

查看答案和解析>>
科目:初中数学 来源: 题型:
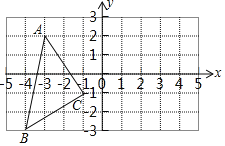
【题目】如图,在平面直角坐标系中,△ABC的顶点A、B、C坐标分别为(﹣3,2),(﹣4,﹣3),(﹣1,﹣1).
(1)画出△ABC关于y轴对称的△A1B1C1;(A、B、C的对称点分别为A1、B1、C1)
(2)写出△A1B1C1各顶点A1、B1、C1的坐标.A1 、B1 、C1
(3)直接写出△ABC的面积= .
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com