
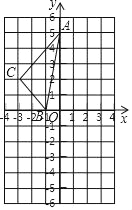
【题目】如图,在平面直角坐标系中,A(0,5)、B(﹣1,0)、C(﹣3,2).
(1)请画出将△ABC向右平移4个单位得到的△A1B1C1.
(2)请画出将△ABC关于点O成中心对称的△A2B2C2.
(3)请直接写出△A1B1C1与△A2B2C2的对称中心的坐标.
科目:初中数学 来源: 题型:
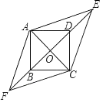
【题目】如图,四边形ABCD是边长为1的正方形,E,F为BD所在直线上的两点.若AE= ![]() ,∠EAF=135°,则以下结论正确的是( )
,∠EAF=135°,则以下结论正确的是( )
A. DE=1 B. tan∠AFO= ![]() C. AF=
C. AF= ![]() D. 四边形AFCE的面积为
D. 四边形AFCE的面积为 ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
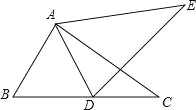
【题目】已知:如图,点B、D、C在一条直线上,AB=AD,BC=DE,AC=AE,
(1)求证:∠EAC=∠BAD.
(2)若∠BAD=42°,求∠EDC的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
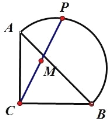
【题目】如图,在等腰 Rt△ABC 中,AC=BC=2,点 P 在以斜边 AB 为直径的半圆上,M 为 PC 的中点.当点 P 沿半圆从点A 运动至点 B 时,点 M 运动的路径长是_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
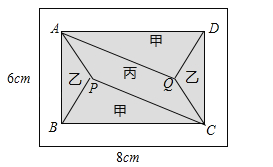
【题目】(2017浙江省温州市)小黄准备给长8m,宽6m的长方形客厅铺设瓷砖,现将其划分成一个长方形ABCD区域Ⅰ(阴影部分)和一个环形区域Ⅱ(空白部分),其中区域Ⅰ用甲、乙、丙三种瓷砖铺设,且满足PQ∥AD,如图所示.
(1)若区域Ⅰ的三种瓷砖均价为300元/m2,面积为S(m2),区域Ⅱ的瓷砖均价为200元/m2,且两区域的瓷砖总价为不超过12000元,求S的最大值;
(2)若区域Ⅰ满足BC=2:3,区域Ⅱ四周宽度相等.
①求AB,BC的长;
②若甲、丙两瓷砖单价之和为300元/m2,乙、丙瓷砖单价之比为5:3,且区域Ⅰ的三种瓷砖总价为4800元,求丙瓷砖单价的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某市每年都举行“希望杯”篮球赛,去年初赛阶段,共15支队伍参赛,每两队之间都比赛一场,下表是去年初赛部分队伍的积分榜.
队名 | 比赛场次 | 胜场 | 负场 | 积分 |
A | 14 | 10 | 4 | 24 |
B | 14 | 9 | 5 | 23 |
C | 14 | 4 | 10 | 18 |
D | 14 | 0 | 14 | 14 |
(1)去年某队的总积分为20分,则该队在比赛中胜了多少场?
(2)今年,参赛的队伍比去年有所增加,但因场地受限,组委会决定初赛阶段共安排40场比赛,并将参赛队伍平均分成4个小组,各小组每两队之间都比赛一场,求今年比去年增加了多少支队伍?
查看答案和解析>>
科目:初中数学 来源: 题型:
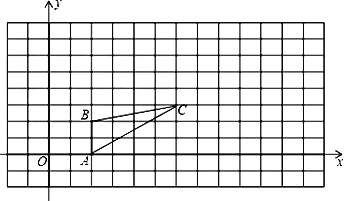
【题目】如图,图中的小方格都是边长为1的正方形,△ABC的A、B、C三点坐标为A(2,0)、B(2,2)、C(6,3)。
(1) 请在图中画出一个△![]() ,使△
,使△![]() 与△ABC是以坐标原点为位似中心,相似比为2的位似图形。
与△ABC是以坐标原点为位似中心,相似比为2的位似图形。
(2)求△![]() 的面积。
的面积。
查看答案和解析>>
科目:初中数学 来源: 题型:
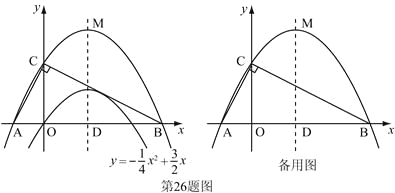
【题目】(本题满分12分)已知二次函数![]() 的图象如图.
的图象如图.
(1)求它的对称轴与![]() 轴交点D的坐标;
轴交点D的坐标;
(2)将该抛物线沿它的对称轴向上平移,设平移后的抛物线与![]() 轴,
轴,![]() 轴的交点分别为A、B、C三点,若∠ACB=90°,求此时抛物线的解析式;
轴的交点分别为A、B、C三点,若∠ACB=90°,求此时抛物线的解析式;
(3)设(2)中平移后的抛物线的顶点为M,以AB为直径,D为圆心作⊙D,试判断直线CM与⊙D的位置关系,并说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com