
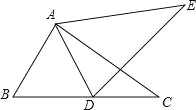
【题目】已知:如图,点B、D、C在一条直线上,AB=AD,BC=DE,AC=AE,
(1)求证:∠EAC=∠BAD.
(2)若∠BAD=42°,求∠EDC的度数.
【答案】(1)见解析 (2)42°.
【解析】试题分析:(1)利用“边边边”证明△ABC和△ADE全等,根据全等三角形对应角相等可得∠BAC=∠DAE,然后都减去∠CAD即可得证;
(2)根据全等三角形对应角相等可得∠B=∠ADE,再根据三角形的一个外角等于与它不相邻的两个内角的和列式求出∠EDC=∠BAD,从而得解.
试题解析:(1)证明:在△ABC和△ADE中,
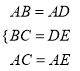 ,
,
∴△ABC≌△ADE(SSS),
∴∠BAC=∠DAE,
∴∠DAE﹣∠CAD=∠BAC﹣∠CAD,
即:∠EAC=∠BAD;
(2)∵△ABC≌△ADE,
∴∠B=∠ADE,
由三角形的外角性质得,∠ADE+∠EDC=∠BAD+∠B,
∴∠EDC=∠BAD,
∴∠BAD=42°,
∴∠EDC=42°.


科目:初中数学 来源: 题型:
【题目】如图,在不等边△ABC中,PM⊥AB于点M,PN⊥AC于点N,且PM=PN,Q在AC上,PQ=QA,MP=3,△AMP的面积是6,下列结论:①AM<PQ+QN,②QP∥AM,③△BMP≌△PQC,④∠QPC+∠MPB=90°,⑤△PQN的周长是7,其中正确的有( )个.
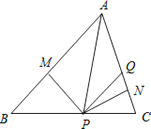
A. 1 B. 2 C. 3 D. 4
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知任意三角形的三边长,如何求三角形面积?
古希腊的几何学家海伦解决了这个问题,在他的著作《度量论》一书中给出了计算公式﹣﹣海伦公式S=![]() (其中a,b,c是三角形的三边长,p=
(其中a,b,c是三角形的三边长,p=![]() ,S为三角形的面积),并给出了证明
,S为三角形的面积),并给出了证明
例如:在△ABC中,a=3,b=4,c=5,那么它的面积可以这样计算:
∵a=3,b=4,c=5
∴p=![]() =6
=6
∴S=![]() =
=![]() =6
=6
事实上,对于已知三角形的三边长求三角形面积的问题,还可用我国南宋时期数学家秦九韶提出的秦九韶公式等方法解决.
如图,在△ABC中,BC=5,AC=6,AB=9
(1)用海伦公式求△ABC的面积;
(2)求△ABC的内切圆半径r.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图:在△ABC中,BE、CF分别是AC、AB两边上的高,在BE上截取BD=AC,在CF的延长线上截取CG=AB,连接AD、AG.
(1)求证:AD=AG;
(2)AD与AG的位置关系如何,请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】关于ABCD的叙述,正确的是( )
A. 若AC⊥BD,则ABCD是正方形
B. 若AC=BD,则ABCD是正方形
C. 若AB⊥BC,则ABCD是菱形
D. 若AB=BC,则ABCD是菱形
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】解答题。
(1)计算:18+42÷(﹣2)﹣(﹣3)2×5.
(2)化简求值:(5xy﹣8x2)﹣(﹣12x2+4xy),其中x=﹣0.5,y=2.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某向在静水中的航行速度为每小时a千米,水流速度为每小时b千米,轮船顺水航行的速度是________,逆水航行的速度_______________.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com