
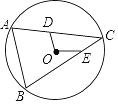
【题目】如图,点C是⊙O上一点,⊙O的半径为![]() ,D、E分别是弦AC、BC上一动点,且OD=OE=
,D、E分别是弦AC、BC上一动点,且OD=OE=![]() ,则AB的最大值为( )
,则AB的最大值为( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
【答案】A
【解析】
先判断出OD⊥AC、OE⊥BC时∠ACB最大,从而得到AB最大,连接OC,根据直角三角形30°角所对的直角边等于斜边的一半求出∠ACO=30°,再根据垂径定理和勾股定理求出AC,然后求出∠ACB=60°,再求出AC=BC,从而得到△ABC是等边三角形,最后根据等边三角形的性质可得AB=AC.
:
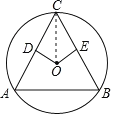
如图,当OD⊥AC、OE⊥BC时∠ACB最大,AB最大,
连接OC,
∵O的半径为2![]() ,OD=
,OD=![]() ,
,
∴∠ACO=30°,
∴AC=2CD=2![]() =2
=2![]() =2
=2![]() ,
,
同理可得∠BOC=30°,
∴∠ACB=60°,
∵OD=OE,OD⊥AC、OE⊥BC,∴AC=BC,
∴△ABC是等边三角形,
∴AB=AC=2![]() ,
,
即AB的最大值为2![]() .
.
故答案选A.


科目:初中数学 来源: 题型:
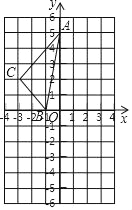
【题目】如图,在平面直角坐标系中,A(0,5)、B(﹣1,0)、C(﹣3,2).
(1)请画出将△ABC向右平移4个单位得到的△A1B1C1.
(2)请画出将△ABC关于点O成中心对称的△A2B2C2.
(3)请直接写出△A1B1C1与△A2B2C2的对称中心的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
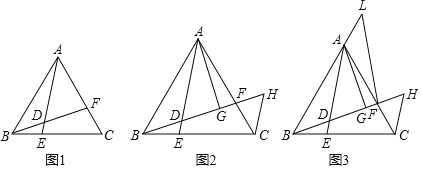
【题目】△ABC是等边三角形,点E、F分别是边BC、AC上的点,且BE=CF,AE、BF交于点D.
(1)如图1,求证:AE=BF.
(2)如图2,过点A作AG⊥BF于点G,过点C作CH∥AE交BF延长线于点H,若D为BG中点,求BH:CH的值;
(3)如图3,在(2)的条件下,L为BA延长线上一点,且FL=FB,△FLA的面积为2,求△ABC的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,某幢大楼顶部有广告牌CD,小宇身高MA为1.89米,他站在立在离大楼45米的A处测得大楼顶端点D的仰角为30°;接着他向大楼前进15米,站在点B处测得广告牌顶端点C的仰角为45°.
(1)求这幢大楼的高DH;
(2)求这块广告牌CD的高度.(取![]() ≈1.732,计算结果保留一位小数)
≈1.732,计算结果保留一位小数)

查看答案和解析>>
科目:初中数学 来源: 题型:
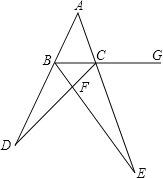
【题目】如图,在![]() 中,
中,![]() 平分
平分![]() 交
交![]() 于点
于点![]() ,延长
,延长![]() 至点
至点![]() 平分
平分![]() ,且
,且![]() 的延长线交于点
的延长线交于点![]() ,若
,若![]() .
.
![]() 求证:
求证:![]() ;
;
![]() 求
求![]() 的度数;
的度数;
![]() 若在图中继续作
若在图中继续作![]() 与
与![]() 的平分线交于点
的平分线交于点![]() ,作
,作![]() 与
与![]() 的平分线交于点
的平分线交于点![]() ,作
,作![]() 与
与![]() 的平分线交于点
的平分线交于点![]() ,以此类推,作
,以此类推,作![]() 与
与![]() 的平分线交于点
的平分线交于点![]() ,请用含有
,请用含有![]() 的式了表示
的式了表示![]() 的度数(直接写答案).
的度数(直接写答案).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知A、B两点的坐标分别为(2,0)、(0,4),P是△AOB外接圆⊙C上的一点,且∠AOP=45°,则点P的坐标为________.
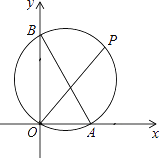
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在⊙O的内接四边形ABCD中,AB=AD,∠C=120°,点E在⊙O上.
(1)求∠AED的度数;
(2)若⊙O的半径为2,则![]() 的长为多少?
的长为多少?
(3)连接OD,OE,当∠DOE=90°时,AE恰好是⊙O的内接正n边形的一边,求n的值.

查看答案和解析>>
科目:初中数学 来源: 题型:
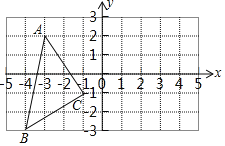
【题目】如图,在平面直角坐标系中,△ABC的顶点A、B、C坐标分别为(﹣3,2),(﹣4,﹣3),(﹣1,﹣1).
(1)画出△ABC关于y轴对称的△A1B1C1;(A、B、C的对称点分别为A1、B1、C1)
(2)写出△A1B1C1各顶点A1、B1、C1的坐标.A1 、B1 、C1
(3)直接写出△ABC的面积= .
查看答案和解析>>
科目:初中数学 来源: 题型:
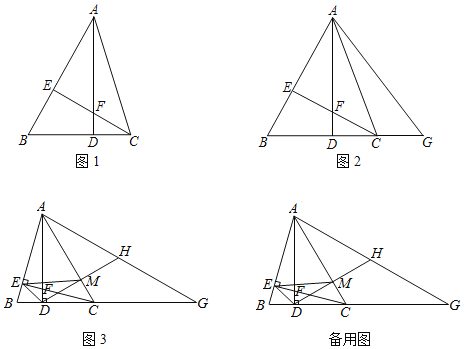
【题目】如图1,在△ABC中,AD⊥BC于D,CE⊥AB于E,AD与CE交于点F,∠ACE=45°.
(1)求证:BE=EF;
(2)如图2,G在BC的延长线上,连接GA,若GA=GB,求证:AC平分∠DAG;
(3)如图3,在(2)的条件下,H为AG的中点,连接DH交AC于M,连接EM、ED,若S△EMC=4,∠BAD=15°,求AM的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com