
【题目】如图1,在△ABC中,AD⊥BC于D,CE⊥AB于E,AD与CE交于点F,∠ACE=45°.
(1)求证:BE=EF;
(2)如图2,G在BC的延长线上,连接GA,若GA=GB,求证:AC平分∠DAG;
(3)如图3,在(2)的条件下,H为AG的中点,连接DH交AC于M,连接EM、ED,若S△EMC=4,∠BAD=15°,求AM的长.
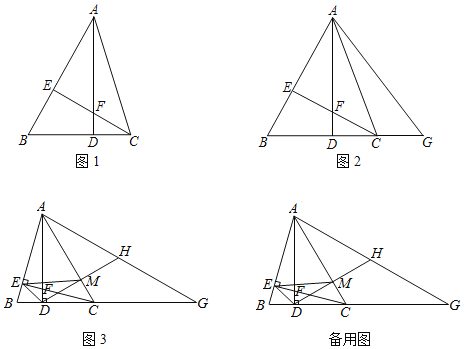
【答案】(1)见解析;(2)见解析;(3)AM=6.
【解析】
(1)先判断出AE=CE,再利用等角的余角相等判断出∠EAF=∠ECB,进而判断出△AEF≌△CEB,即可得出结论;
(2)先利用三角形外角的性质得出∠AEF=45°+∠CAD,进而得出∠B=45°+∠CAD,而∠B=∠BAG,得出∠BAG=45°+∠CAD,而∠BAG=45°+∠CAG,即可得出结论;
(3)先判断出△ADH是等边三角形,进而利用含30度角的直角三角形的性质判断出AM=3CM,进而求出△ACM的面积,即可求出AE,进而求出AC,即可得出结论.
解:(1)∵CE⊥AB,
∴∠AEC=∠BEC=90°,
∵∠ACE=45°,
∴∠CAE=45°=∠ACE,
∴AE=CE,
∵AD⊥BC,
∴∠ADC=90°,
∴∠ECB+∠CFD=90°,
∵∠CFD=∠AFE,
∴∠ECB+∠AFE=90°,
∵∠EAF+∠AFE=90°,
∴∠EAF=∠ECB,
∵∠AEF=∠CEB=90°,
∴△AEF≌△CEB(ASA),
∴BE=EF;
(2)∵△AEF≌△CEB,
∴∠AFE=∠B,
∵∠AFE=∠ACE+∠CAD=45°+∠CAD,
∴∠B=45°+∠CAD,
∵AG=BG,
∴∠B=∠BAG,
∴∠BAG=45°+∠CAD,
∵∠BAG=∠CAE+∠CAG=45°+∠CAG,
∴∠CAD=∠CAG,
∴AC平分∠DAG;
(3)∵∠BAD=15°,∠CAE=45°,
∴∠CAD=∠CAE﹣∠BAD=30°,
∵∠CAD=∠CAG,
∴∠DAG=2∠CAD=60°,
在Rt△ADG中,点H是AG的中点,
∴DH=AH,
∴△ADH是等边三角形,
∴∠ADH=60°,AD=AH,
∵∠CAD=∠CAG,
∴AC⊥DH,
即:∠AMD=∠DMC=90°
∵∠ADC=90°,
∴∠CDM=30°,
在Rt△DMC中,CD=2CM,DM=![]() CM,
CM,
在Rt△AMD中,AM=![]() DM=
DM=![]() ×
×![]() CM=3CM,
CM=3CM,
∴S△AEM=3S△CEM=3×4=12,
∴S△ACE=S△CEM+S△AEM=16,
∵∠AEC=90°,AE=CE,
∴S△ACE=![]() AE2=16,
AE2=16,
∴AE=4![]() ,
,
∴AC=![]() AE=8,
AE=8,
∴AM+CM=8,
∵AM=3CM,
∴3CM+CM=8,
∴CM=2,
∴AM=3CM=6.


 口算题卡北京妇女儿童出版社系列答案
口算题卡北京妇女儿童出版社系列答案科目:初中数学 来源: 题型:
【题目】如图(1),在□ABCD中,P是CD边上的一点,AP与BP分别平分∠DAB和∠CBA。
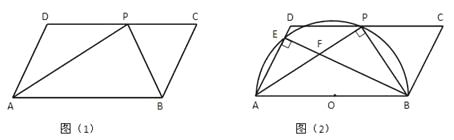
【1】判断△APB是什么三角形?证明你的结论;
【2】比较DP与PC的大小;
【3】如图(2)以AB为直径作半圆O,交AD于点E,连结BE与AP交于点F,若AD=5cm,AP=8cm,求证△AEF∽△APB,并求tan∠AFE的值。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,把抛物线y=![]() x2平移得到抛物线m,抛物线m经过点A(﹣6,0)和原点O(0,0),它的顶点为P,它的对称轴与抛物线y=
x2平移得到抛物线m,抛物线m经过点A(﹣6,0)和原点O(0,0),它的顶点为P,它的对称轴与抛物线y=![]() x2交于点Q,则图中阴影部分的面积为 ▲ .
x2交于点Q,则图中阴影部分的面积为 ▲ .

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,长为60cm,宽为x(cm)的大长方形被分割为7小块,除阴影 A, B外,其余5块是形状、大小完全相同的小长方形,其较短一边长为 y (cm).

(1)填空:从图可知,每个小长方形较长的一边长是_________cm (用含y的代数式表示).
(2)分别求出阴影 A,B的面积,并计算阴影 A,B的面积差?(用含x,y的式子表示)
(3)当y=10时,阴影 A与阴影 B的面积差会随着x的变化而变化吗?请你作出判断,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】对角线长分别为6和8的菱形ABCD如图所示,点O为对角线的交点,过点O折叠菱形,使B,B′两点重合,MN是折痕.若B'M=1,则CN的长为( )
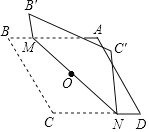
A. 7 B. 6 C. 5 D. 4
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在环境创优活动中,某居民小区要在一块靠墙(墙长25米)的空地上修建一个矩形养鸡场,养鸡场的一边靠墙,如果用60m长的篱笆围成中间有一道篱笆的养鸡场,设养鸡场平行于墙的一边BC的长为x(m),养鸡场的面积为y(m2)
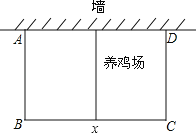
(1)求y与x之间的函数关系式,并写出自变量x的取值范围;
(2)养鸡场的面积能达到300m2吗?若能,求出此时x的值,若不能,说明理由;
(3)根据(1)中求得的函数关系式,判断当x取何值时,养鸡场的面积最大?最大面积是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(10分)如图,已知△ABC为等边三角形,点D、E分别在BC、AC边上,且AE=CD,AD与BE相交于点F。

(1)求证:△ABE≌△CAD;(2)求∠BFD的度数。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com