
【题目】已知△ABC与△ABD不全等,且AC=AD=1,∠ABD=∠ABC=45°,∠ACB=60°,则CD= .
【答案】1或![]() .
.
【解析】分析:
由题意可知本题存在两种可能情况:(1)如图1,C、D两点在线段AB的同侧,此时由已知条件易证△ACD是等边三角形,由此即可求得CD的长;(2)如图2,C、D两点在线段AB的两侧,此时由已知条件可知将△ABD沿AB翻折,点D的对应点D′刚好落在BC边上,连接CD,由已知条件可证得∠CAD=90°,从而可在Rt△ACD中由勾股定理求得CD的长.
详解:
(1)如图1,当C、D在AB同侧时,
∵AC=AD=1,∠C=60°,
∴△ACD是等边三角形,
∴CD=AC=1;
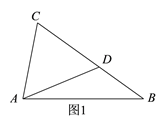
(2)如图2,当C、D在AB两侧时,
∵∠ABC=∠ABD=45°,
∴把△ABD沿AB翻折得到△ABD′时,点D′在BC边上,
由(1)可知,此时△ACD′是等边三角形,
∴∠AD′C=60°,
∴∠AD′B=120°,
∴∠ADB=120°,
又∵在四边形ADBC中,∠ACB=60°,∠DBC=∠ABC+∠ABD=90°,
∴∠CAD=360°-60°-120°-90°=90°,
∴在Rt△ACD中,CD=![]() .
.

综上所述可得CD的长为1或![]() .
.
故答案为:1或![]() .
.


科目:初中数学 来源: 题型:
【题目】随着科技的迅猛发展,人与人之间的沟通方式更多样、便捷某校数学兴趣小组设计了“你最喜欢的沟通方式”调查问卷(每人必选且只选一种),在全校范围内随机调查了部分学生,将统计结果绘制了如下两幅不完整的统计图,请结合图中所给的信息解答下列问题.
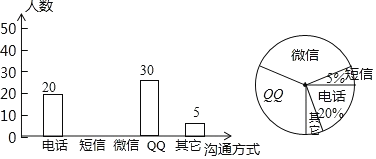
(1)这次统计共抽查了______名学生;在扇形统计图中,表示“QQ”的扇形圆心角的度数为________;
(2)将条形统计图补充完整;
(3)该校共有2500名学生,请估计该校最喜欢用“微信”进行沟通的学生有多少名?
(4)某天甲、乙两名同学都想从“微信”“QQ”“电话”三种沟通方式中选一种方式与对方联系,请用列表或画树状图的方法求出甲、乙两名同学恰好选择同一种沟通方式的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图①,P为△ABC所在平面上一点,且∠APB=∠BPC=∠CPA=120°,则点P叫作△ABC的费马点.
(1)如果点P为锐角△ABC的费马点,且∠ABC=60°.
①求证: △ABP∽△BCP;
②若PA=3,PC=4,求PB的长;
(2)如图②,已知锐角△ABC,分别以AB,AC为边向外作正△ABE和正△ACD,CE和BD相交于点P,连接AP.
①求∠CPD的度数;
②求证:点P为△ABC的费马点.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下面两个多位数1248624…… ,6248624…… ,都是按照如下方法得到的:将第一位数字乘以2,若积为一位数,将其写在第2位上,若积为两位数,则将其个位数字写在第2位.对第2位数字再进行如上操作得到第3位数字……,后面的每一位数字都是由前一位数字进行如上操作得到的.当第1位数字是3时,仍按如上操作得到一个多位数,则这个多位数前100位的所有数字之和是( )
A. 495 B. 497 C. 501 D. 503
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校九年级有1200名学生,在体育考试前随机抽取部分学生进行跳绳测试,根据测试成绩制作了下面两个统计图.请根据相关信息,解答下列问题:

(Ⅰ)本次参加跳绳测试的学生人数为___________,图①中![]() 的值为___________;
的值为___________;
(Ⅱ)求本次调查获取的样本数据的平均数、众数和中位数;
(Ⅲ)根据样本数据,估计该校九年级跳绳测试中得3分的学生约有多少人?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知数轴上两点A,B表示的数分别为﹣2,6,用符号“AB”来表示点A和点B之间的距离.
![]()
(1)求AB的值;
(2)若在数轴上存在一点C,使AC=3BC,求点C表示的数;
(3)在(2)的条件下,点C位于A、B两点之间.点A以1个单位/秒的速度沿着数轴的正方向运动,2秒后点C以2个单位/秒的速度也沿着数轴的正方向运动,到达B点处立刻返回沿着数轴的负方向运动,直到点A到达点B,两个点同时停止运动.设点A运动的时间为t,在此过程中存在t使得AC=3BC仍成立,求t的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知,在正方形ABCD中,点E在边AD上,点F在边BC的延长线上,且AE=CF,连接AC,EF.
(1)如图①,求证:EF//AC;
(2)如图②,EF与边CD交于点G,连接BG,BE,
①求证:△BAE≌△BCG;
②若BE=EG=4,求△BAE的面积.
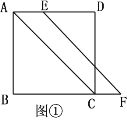
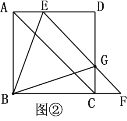
查看答案和解析>>
科目:初中数学 来源: 题型:
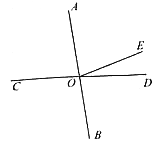
【题目】如图,AB、CD交于点O,∠AOE=4∠DOE,∠AOE的余角比∠DOE小10°(题中所说的角均是小于平角的角).
(1)求∠AOE的度数;
(2)请写出∠AOC在图中的所有补角;
(3)从点O向直线AB的右侧引出一条射线OP,当∠COP=∠AOE+∠DOP时,求∠BOP的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
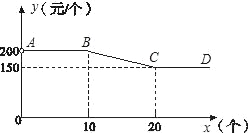
【题目】永定土楼是世界文化遗产“福建土楼”的组成部分,是闽西的旅游胜地.“永定土楼”模型深受游客喜爱.图中折线(AB∥CD∥x轴)反映了某种规格土楼模型的单价y(元)与购买数量x(个)之间的函数关系.
(1)求当10≤x≤20时,y与x的函数关系式;
(2)已知某旅游团购买该种规格的土楼模型总金额为2625元,问该旅游团共购买这种土楼模型多少个?(总金额=数量×单价)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com