练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    【题目】永定土楼是世界文化遗产“福建土楼”的组成部分，是闽西的旅游胜地．“永定土楼”模型深受游客喜爱．图中折线（AB∥CD∥x轴）反映了某种规格土楼模型的单价y（元）与购买数量x（个）之间的函数关系．

    （1）求当10≤x≤20时，y与x的函数关系式；

    （2）已知某旅游团购买该种规格的土楼模型总金额为2625元，问该旅游团共购买这种土楼模型多少个？（总金额=数量×单价）

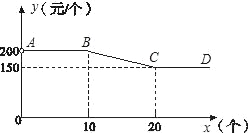
    【答案】（1）当10≤x≤20时，y=﹣5x+250；（2）旅游团共购买这种土楼模型15个

    【解析】分析：(1)设出一次函数解析式,把B、C两点的坐标代入可得所求函数关系式;

    (2)所用金额既不是200的倍数,也不是150的倍数,可得模型的单价在150和200之间,根据总价等于2625得到一元二次方程,求解即可.

    详解：（1）当10≤x≤20时，设y=kx+b（k≠0）

    依题意，得

    解得

    ∴当10≤x≤20时，y=﹣5x+250；

    （2）∵10×200＜2625＜20×150

    ∴10＜x＜20（8分）

    依题意，得xy=x（﹣5x+250）=2625

    即x2﹣50x+525=0

    解得x1=15，x2=35（舍去）

    ∴只取x=15．（12分）

    答：该旅游团共购买这种土楼模型15个．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    【题目】已知△ABC与△ABD不全等，且AC=AD=1，∠ABD=∠ABC=45°，∠ACB=60°，则CD=　 　．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】计算：

    （1）23﹣17﹣（﹣7）+（﹣16）

    （2）

    （3）﹣22÷（﹣4）3+|0.8﹣1|×（2）2

    （4）4xy+（3y2﹣2x2）﹣（5xy﹣2x2）﹣4y2

    （5）先化简，再求值：x﹣2（x﹣y2）+（﹣x+y2），其中x＝﹣，y＝3

    查看答案和解析>>

    科目：初中数学 来源： 题型：

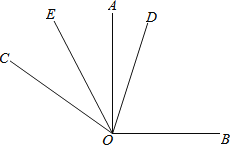
    【题目】如图，已知同一平面内∠AOB＝90°，∠AOC＝60°．

    （1）问题发现：∠BOD的余角是　 ，∠BOC的度数是 　；

    （2）拓展探究：若OD平分∠BOC，OE平分∠AOC，则∠DOE的度数是　　；

    （3）类比延伸：在（2）条件下，如果将题目中的∠AOB＝90°改为∠AOB＝2∠β；∠AOC＝60°改为∠AOC＝2α（α＜45°），其他条件不变，你能求出∠DOE吗？若能，请你写出求解过程：若不能，请说明理由．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

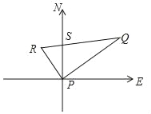
    【题目】如图，某港口P位于东西方向的海岸线上，A、B两艘轮船同时从港口P出发，各自沿一固定方向航行，A轮船每小时航行12海里，B轮船每小时航行16海里．它们离开港口一个半小时后分别位于点R、Q处，且相距30海里．已知B轮船沿北偏东60°方向航行．

    （1）A轮船沿哪个方向航行？请说明理由；

    （2）请求出此时A轮船到海岸线的距离．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，在数轴上点A表示数a，点C表示数c，且.我们把数轴上两点之间的距离用表示两点的大写字母一起标记.

    比如，点A与点B之间的距离记作AB.

    (1)求AC的值；

    (2)若数轴上有一动点D满足CD＋AD=36，直接写出D点表示的数；

    (3)动点B从数1对应的点开始向右运动，速度为每秒1个单位长度，同时点A，C在数轴上运动，点A、C的速度分别为每秒 3个单位长度，每秒4个单位长度，运动时间为t秒.

    ①若点A向右运动，点C向左运动，AB=BC，求t的值.

    ②若点A向左运动，点C向右运动，2AB－m×BC的值不随时间t的变化而改变，请求出m的值.

    查看答案和解析>>

    科目：初中数学 来源： 题型：

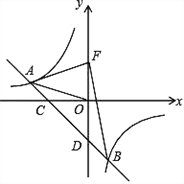
    【题目】如图，一次函数 yax 2(a0) 的图象与反比例函数 y(k0) 的图象交于 A、B两点，且与x轴、y轴分别交于点C、D．已知 tan∠AOC=，AO=．

    （1）求这个一次函数和反比例函数的解析式；

    （2） 若点 F 是点D 关于 x 轴的对称点，求△ABF 的面积．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图1，在△ABC中，AB=AC，以△ABC的边AB为直径的⊙O角边BC于点E，过点E作DE⊥AC交AC于D．

    （1）求证：DE是⊙O的切线；

    （2）如图2，若线段AB、DE的延长线交于点F，∠C=75°，CD=2﹣，求⊙O的半径和EF的长．

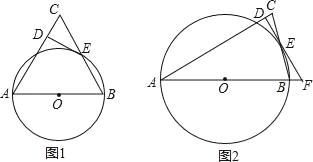
    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】△ABC中，∠BAC=90°，AB=AC，点D为直线BC上一动点（点D不与B，C重合），以AD为边在AD右侧作正方形ADEF，连接CF．

    （1）观察猜想

    如图1，当点D在线段BC上时，

    ①BC与CF的位置关系为：　 　．

    ②BC，CD，CF之间的数量关系为：　 　；（将结论直接写在横线上）

    （2）数学思考

    如图2，当点D在线段CB的延长线上时，结论①，②是否仍然成立？若成立，请给予证明；若不成立，请你写出正确结论再给予证明．

    （3）拓展延伸

    如图3，当点D在线段BC的延长线上时，延长BA交CF于点G，连接GE．若已知AB=2，CD=BC，请求出GE的长．

    查看答案和解析>>

    同步练习册答案