
【题目】△ABC中,∠BAC=90°,AB=AC,点D为直线BC上一动点(点D不与B,C重合),以AD为边在AD右侧作正方形ADEF,连接CF.
(1)观察猜想
如图1,当点D在线段BC上时,
①BC与CF的位置关系为: .
②BC,CD,CF之间的数量关系为: ;(将结论直接写在横线上)
(2)数学思考
如图2,当点D在线段CB的延长线上时,结论①,②是否仍然成立?若成立,请给予证明;若不成立,请你写出正确结论再给予证明.
(3)拓展延伸
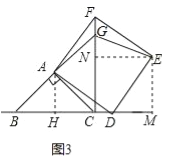
如图3,当点D在线段BC的延长线上时,延长BA交CF于点G,连接GE.若已知AB=2![]() ,CD=
,CD=![]() BC,请求出GE的长.
BC,请求出GE的长.

【答案】(1)CF⊥BD,BC=CF+CD;(2)成立,证明详见解析;(3)![]() .
.
【解析】试题分析:(1)①根据正方形的性质得到∠BAC=∠DAF=90°,推出△DAB≌△FAC,根据全等三角形的性质即可得到结论;②由正方形ADEF的性质可推出△DAB≌△FAC,根据全等三角形的性质得到CF=BD,∠ACF=∠ABD,根据余角的性质即可得到结论;(2)根据正方形的性质得到∠BAC=∠DAF=90°,推出△DAB≌△FAC,根据全等三角形的性质即可得到结论(3)根据等腰直角三角形的性质得到BC=![]() AB=4,AH=
AB=4,AH=![]() BC=2,求得DH=3,根据正方形的性质得到AD=DE,∠ADE=90°,根据矩形的性质得到NE=CM,EM=CN,由角的性质得到∠ADH=∠DEM,根据全等三角形的性质得到EM=DH=3,DM=AH=2,等量代换得到CN=EM=3,EN=CM=3,根据等腰直角三角形的性质得到CG=BC=4,根据勾股定理即可得到结论.
BC=2,求得DH=3,根据正方形的性质得到AD=DE,∠ADE=90°,根据矩形的性质得到NE=CM,EM=CN,由角的性质得到∠ADH=∠DEM,根据全等三角形的性质得到EM=DH=3,DM=AH=2,等量代换得到CN=EM=3,EN=CM=3,根据等腰直角三角形的性质得到CG=BC=4,根据勾股定理即可得到结论.
试题解析:解:(1)①正方形ADEF中,AD=AF,
∵∠BAC=∠DAF=90°,
∴∠BAD=∠CAF,
在△DAB与△FAC中,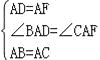 ,
,
∴△DAB≌△FAC,
∴∠B=∠ACF,
∴∠ACB+∠ACF=90°,即CF⊥BD;
②△DAB≌△FAC,
∴CF=BD,
∵BC=BD+CD,
∴BC=CF+CD;
(2)成立,
∵正方形ADEF中,AD=AF,
∵∠BAC=∠DAF=90°,
∴∠BAD=∠CAF,
在△DAB与△FAC中,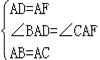 ,
,
∴△DAB≌△FAC,
∴∠B=∠ACF,CF=BD
∴∠ACB+∠ACF=90°,即CF⊥BD;
∵BC=BD+CD,
∴BC=CF+CD;
(3)解:过A作AH⊥BC于H,过E作EM⊥BD于M,EN⊥CF于N,
∵∠BAC=90°,AB=AC,
∴BC=![]() AB=4,AH=
AB=4,AH=![]() BC=2,
BC=2,
∴CD=![]() BC=1,CH=
BC=1,CH=![]() BC=2,
BC=2,
∴DH=3,
由(2)证得BC⊥CF,CF=BD=5,
∵四边形ADEF是正方形,
∴AD=DE,∠ADE=90°,
∵BC⊥CF,EM⊥BD,EN⊥CF,
∴四边形CMEN是矩形,
∴NE=CM,EM=CN,
∵∠AHD=∠ADC=∠EMD=90°,
∴∠ADH+∠EDM=∠EDM+∠DEM=90°,
∴∠ADH=∠DEM,
在△ADH与△DEM中,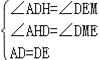 ,
,
∴△ADH≌△DEM,
∴EM=DH=3,DM=AH=2,
∴CN=EM=3,EN=CM=3,
∵∠ABC=45°,
∴∠BGC=45°,
∴△BCG是等腰直角三角形,
∴CG=BC=4,
∴GN=1,
∴EG=![]() =
=![]() .
.


科目:初中数学 来源: 题型:
【题目】四张扑克牌(方块2、黑桃4、黑桃5、梅花5)的牌面如图l,将扑克牌洗匀后,如图2背面朝上放置在桌面上.小亮和小明设计的游戏规则是两人同时抽取一张扑克牌,两张牌面数字之和为奇数时,小亮获胜;否则小明获胜.请问这个游戏规则公平吗?并说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图E、F分别在正方形ABCD的边BC、CD上,且∠EAF=45°.
(1)求证:EF=BE+DF;
(2)若线段EF、AB的长分别是方程x2﹣5x+6=0的两个根,求△AEF的面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某射手在同一条件下进行射击,结果如下表所示:

(1)计算并填写表中击中靶心的频率;(结果保留三位小数)
(2)这个射手射击一次,击中靶心的概率估计值是多少?(结果保留两位小数)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】黄冈某地“杜鹃节”期间,某公司70名职工组团前往参观欣赏,旅游景点规定:①门票每人60元,无优惠;②上山游玩可坐景点观光车,观光车有四座和十一座车,四座车每辆60元,十一座车每人10元.公司职工正好坐满每辆车且总费用不超过5000元,问公司租用的四座车和十一座车各多少辆?
查看答案和解析>>
科目:初中数学 来源: 题型:
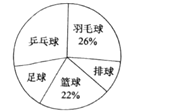
【题目】某中学为了了解学生最喜欢的一种球类运动,以便合理安排活动场地,在全校至少喜欢一种球类(乒乓球、羽毛球、排球、篮球、足球)运动的1500名学生中,随机抽取了若干名学生进行调查(每人只能在这五种球类运动中选择一种).调查结果统计如下:
球类名称 | 人数 |
乒乓球 | 42 |
羽毛球 | a |
排球 | 15 |
篮球 | 33 |
足球 | b |
![]()
解答下列问题:
(1)这次抽样调查中的样本是________;
(2)统计表中,a=________,b=________;
(3)试估计上述1500名学生中最喜欢乒乓球运动的人数.
查看答案和解析>>
科目:初中数学 来源: 题型:
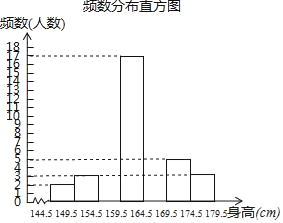
【题目】为了解同学们的身体发育情况,学校体卫办公室对七年级全体学生进行了身高测量(精确到1cm),并从中抽取了部分数据进行统计,请根据尚未完成的频数分布表和频数分布直方图解答下列问题:
频率分布表
分组 | 频数 | 百分比 |
144.5~149.5 | 2 | 4% |
149.5~154.5 | 3 | 6% |
154.5~159.5 | a | 16% |
159.5~164.5 | 17 | 34% |
164.5~169.5 | b | n% |
169.5~174.5 | 5 | 10% |
174.5~179.5 | 3 | 6% |
(1)求a、b、n的值;
(2)补全频数分布直方图;
(3)学校准备从七年级学生中选拔护旗手,要求身高不低于170cm,如果七年级有学生350人,护旗手的候选人大概有多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
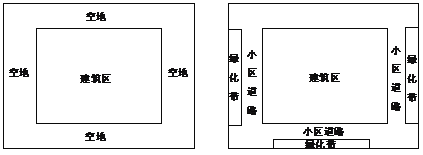
【题目】如左图,某小区的平面图是一个400×300平方米的矩形,正中央的建筑区是与整个小区长宽比例相同的矩形.如果要使四周的空地所占面积是小区面积的36%,并且南北空地与东西空地的宽度各自相同.
(1)求该小区南北空地的宽度;
(2)如右图,该小区在东西南三块空地上做如图所示的矩形绿化带,绿化带与建筑区之间为小区道路,小区道路宽度一致.已知东西侧绿化带完全相同,其长约为200米,南侧绿化带的长为300米,绿化面积为18000平方米,请求出小区道路的宽度.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商店两次购进一批同型号的热水壶和保温杯,第一次购进![]() 个热水壶和
个热水壶和![]() 个保温杯,共用去资金
个保温杯,共用去资金![]() 元,第二次购进
元,第二次购进![]() 个热水壶和
个热水壶和![]() 个保温杯,用去资金
个保温杯,用去资金![]() 元(购买同一商品的价格不变)
元(购买同一商品的价格不变)
(1)求每个热水壶和保温杯的采购单价各是多少元?
(2)若商场计划再购进同种型号的热水壶和保温杯共![]() 个,求所需购货资金
个,求所需购货资金![]() (元)与购买热水壶的数量
(元)与购买热水壶的数量![]() (个)的函数表达式.
(个)的函数表达式.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com