
【题目】如图,在数轴上点A表示数a,点C表示数c,且![]() .我们把数轴上两点之间的距离用表示两点的大写字母一起标记.
.我们把数轴上两点之间的距离用表示两点的大写字母一起标记.
![]()
比如,点A与点B之间的距离记作AB.
(1)求AC的值;
(2)若数轴上有一动点D满足CD+AD=36,直接写出D点表示的数;
(3)动点B从数1对应的点开始向右运动,速度为每秒1个单位长度,同时点A,C在数轴上运动,点A、C的速度分别为每秒 3个单位长度,每秒4个单位长度,运动时间为t秒.
①若点A向右运动,点C向左运动,AB=BC,求t的值.
②若点A向左运动,点C向右运动,2AB-m×BC的值不随时间t的变化而改变,请求出m的值.
【答案】(1)a=-10,b=20 ,A C=30;(2) D:-13 或23;(3) ①![]() 或
或![]() ;②
;②![]()
【解析】
(1)根据非负性可求出答案;
(2)分三种情况:当点D在点A的左侧;当点D在点A,C之间时;当点D在点C的右侧时;进行讨论可求D点表示的数;
(3)①用t的代数式表示AB,BC,列出等式可求解;
②用t的代数式表示AB,BC,代入代数式可求解;
(1)∵|a+10|+(c-20)2=0,
∴a+10=0,c-20=0,
∴a=-10,c=20,
(2)当点D在点A的左侧,
![]()
∵CD+AD=36,
∴AD+AC+AD=36,
∴AD=3,
∴点D点表示的数为-10-3=-13;
当点D在点A,C之间时,
![]()
∵CD+AD=AC=30≠36,
∴不存在点D,使CD+AD=36;
当点D在点C的右侧时,
![]()
∵CD+AD=36,
∴AC+CD+CD=36,
∴CD=3,
∴点D点表示的数为20+3=23;
综上所述,D点表示的数为-13或23;
(3)①∵AB=BC,
∴|(1+t)-(-10+3t)|=|(1+t)-(20-4t)|
∴t=![]() 或
或![]() ;
;
②∵2AB-m×BC=2×(11+4t)-m(19+3t)=(8-3m)t+22-19m,且2AB-m×BC的值不随时间t的变化而改变,
∴8-3m=0,
∴m=![]() .
.


 寒假大串联黄山书社系列答案
寒假大串联黄山书社系列答案科目:初中数学 来源: 题型:
【题目】如图,已知数轴上两点A,B表示的数分别为﹣2,6,用符号“AB”来表示点A和点B之间的距离.
![]()
(1)求AB的值;
(2)若在数轴上存在一点C,使AC=3BC,求点C表示的数;
(3)在(2)的条件下,点C位于A、B两点之间.点A以1个单位/秒的速度沿着数轴的正方向运动,2秒后点C以2个单位/秒的速度也沿着数轴的正方向运动,到达B点处立刻返回沿着数轴的负方向运动,直到点A到达点B,两个点同时停止运动.设点A运动的时间为t,在此过程中存在t使得AC=3BC仍成立,求t的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
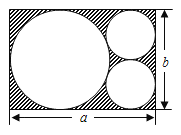
【题目】如图,在一张长为a、宽为b的长方形纸片上,剪掉一个大圆和两个半径相等的小圆.
(1)列出剩余纸片(图中阴影部分)面积的代数式;(结果要求化简)
(2)当a=6cm,b=4cm时,求阴影部分的面积,(π取3.14)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知矩形ABCD,过D作BD的垂线,与BC延长线交于E点,F为BE的中点,连接DF,已知DF=4,设AB=x,AD=y,求代数式x2+(y﹣4)2的值.

查看答案和解析>>
科目:初中数学 来源: 题型:
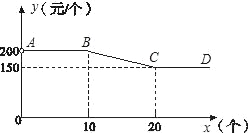
【题目】永定土楼是世界文化遗产“福建土楼”的组成部分,是闽西的旅游胜地.“永定土楼”模型深受游客喜爱.图中折线(AB∥CD∥x轴)反映了某种规格土楼模型的单价y(元)与购买数量x(个)之间的函数关系.
(1)求当10≤x≤20时,y与x的函数关系式;
(2)已知某旅游团购买该种规格的土楼模型总金额为2625元,问该旅游团共购买这种土楼模型多少个?(总金额=数量×单价)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在 A 处观察 C 测得仰角∠CAD=31°,且 A、B 的水平距离 AE=800 米,斜坡 AB 的坡度i 1: 2 ,索道 BC 的坡度i 2 : 3 ,CD⊥AD 于 D,BF⊥CD 于 F,则索道BC 的长大约是( )
(参考数据:tan31°≈0. cos31°≈0.9,![]() ≈3.6)
≈3.6)

A. 1400 B. 1440 C. 1500 D. 1540
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我们知道,任意一个正整数n都可以进行这样的分解:n=p×q(p,q是正整数,且p≤q),在n的所有这种分解中,如果p,q两因数之差的绝对值最小,我们就称p×q是n的最佳分解,并规定:F(n)=![]() ,例如12可以分解成1×12,2×6或3×4,因为12-1>6-2>4-3,所有3×4是最佳分解,所以F(12)=
,例如12可以分解成1×12,2×6或3×4,因为12-1>6-2>4-3,所有3×4是最佳分解,所以F(12)=![]() .
.
(1)如果一个正整数a是另外一个正整数b的平方,我们称正整数a是完全平方数,求证:对任意一个完全平方数m,总有F(m)=1.
(2)如果一个两位正整数t,t=10x+y(1≤x≤y≤9,x,y为自然数),交换其个位上的数与十位上的数得到的新数减去原来的两位正整数所得的差为18,那么我们称这个数t为“吉祥数”,求所有“吉祥数”中F(t)的最大值.
查看答案和解析>>
科目:初中数学 来源: 题型:
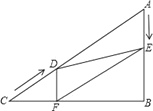
【题目】如图,在Rt△ABC中,∠B=90°,AC=60cm,∠A=60°,点D从点C出发沿CA方向以4cm/秒的速度向点A匀速运动,同时点E从点A出发沿AB方向以2cm/秒的速度向点B匀速运动,当其中一个点到达终点时,另一个点也随之停止运动.设点D、E运动的时间是t秒(0<t≤15).过点D作DF⊥BC于点F,连接DE,EF.
(1)求证:AE=DF;
(2)四边形AEFD能够成为菱形吗?如果能,求出t的值,如果不能,说明理由;
(3)在运动过程中,四边形BEDF能否为正方形?若能,求出t的值;若不能,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】有一座抛物线拱型桥,在正常水位时,水面![]() 的宽为
的宽为![]() 米,拱桥的最高点
米,拱桥的最高点![]() 到水面
到水面![]() 的距离
的距离![]() 为
为![]() 米,点
米,点![]() 是
是![]() 的中点,如图,以点
的中点,如图,以点![]() 为原点,直线
为原点,直线![]() 为
为![]() 轴,建立直角坐标系
轴,建立直角坐标系![]() .
.
(1)求该抛物线的表达式;
(2)如果水面![]() 上升
上升![]() 米(即
米(即![]() )至水面
)至水面![]() ,点
,点![]() 在点
在点![]() 的左侧,
的左侧,
求水面宽度![]() 的长.
的长.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com