练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    【题目】有一座抛物线拱型桥，在正常水位时，水面的宽为米，拱桥的最高点到水面的距离为米，点是的中点，如图，以点为原点，直线为轴，建立直角坐标系.

    （1）求该抛物线的表达式；

    （2）如果水面上升米（即）至水面，点在点的左侧，

    求水面宽度的长.

    【答案】（1）；（2）水面宽度的长为米.

    【解析】分析：（1）根据题意：该抛物线的表达式为：,求出点的坐标，用待定系数法确定函数关系式.

    令 求出点的坐标，即可求出水面宽度的长.

    详解：（1）根据题意：该抛物线的表达式为：

    ∵该抛物线最高点在轴上，，∴点的坐标为

    ∵,点是的中点 ∴点的坐标为 ∴，

    ∴抛物线的表达式为：

    （2）根据题意可知点、点在抛物线上，∥，

    ∵ ， ∴点、点的横坐标都是，

    ∴点坐标为，点坐标为，

    ∴（米）

    答：水面宽度的长为米.

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    【题目】如图，在数轴上点A表示数a，点C表示数c，且.我们把数轴上两点之间的距离用表示两点的大写字母一起标记.

    比如，点A与点B之间的距离记作AB.

    (1)求AC的值；

    (2)若数轴上有一动点D满足CD＋AD=36，直接写出D点表示的数；

    (3)动点B从数1对应的点开始向右运动，速度为每秒1个单位长度，同时点A，C在数轴上运动，点A、C的速度分别为每秒 3个单位长度，每秒4个单位长度，运动时间为t秒.

    ①若点A向右运动，点C向左运动，AB=BC，求t的值.

    ②若点A向左运动，点C向右运动，2AB－m×BC的值不随时间t的变化而改变，请求出m的值.

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，图象中所反映的过程是：张强从家跑步去体育场，在那里锻炼了一阵后，又 去早餐店吃早餐，然后散步走回家，其中 x 表示时间，y 表示张强离家的距离。根据图象提供的信息，以下四个说法错误的是（ ）

    A. 体育场离张强家2.5千米 B. 张强在体育场锻炼了15分钟

    C. 体育场离早餐店4千米 D. 张强从早餐店回家的平均速度是3千米/小时

    查看答案和解析>>

    科目：初中数学 来源： 题型：

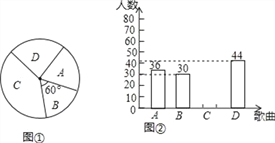
    【题目】为庆祝建军90周年，某校计划在五月份举行“唱响军歌”歌咏比赛，要确定一首喜欢人数最多的歌曲为每班必唱歌曲．为此提供代号为A，B，C，D四首备选曲目让学生选择，经过抽样调查，并将采集的数据绘制如下两幅不完整的统计图．请根据图①，图②所提供的信息，

    解答下列问题：

    （1）本次抽样调查中，选择曲目代号为A的学生占抽样总数的百分比为　　；

    （2）请将图②补充完整；

    （3）若该校共有1260名学生，根据抽样调查的结果估计全校共有多少学生选择喜欢人数最多的歌曲？（要有解答过程）

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】△ABC中，∠BAC=90°，AB=AC，点D为直线BC上一动点（点D不与B，C重合），以AD为边在AD右侧作正方形ADEF，连接CF．

    （1）观察猜想

    如图1，当点D在线段BC上时，

    ①BC与CF的位置关系为：　 　．

    ②BC，CD，CF之间的数量关系为：　 　；（将结论直接写在横线上）

    （2）数学思考

    如图2，当点D在线段CB的延长线上时，结论①，②是否仍然成立？若成立，请给予证明；若不成立，请你写出正确结论再给予证明．

    （3）拓展延伸

    如图3，当点D在线段BC的延长线上时，延长BA交CF于点G，连接GE．若已知AB=2，CD=BC，请求出GE的长．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】某气球内充满了一定量的气体，当温度不变时，气球内气体的气压P（kPa）是气球体积V（m3）的反比例函数，且当V=0.8m3时，P=120kPa。

    （1）求P与V之间的函数表达式；

    （2）当气球内的气压大于100kPa时，气球将爆炸，为确保气球不爆炸，气球的体积应不小于多少？

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】在平面直角坐标系中，O为坐标原点．

    (1)已知点A(3，1)，连接OA，作如下探究：

    探究一：平移线段OA，使点O落在点B，设点A落在点C，若点B的坐标为（1，2），请在图①中作出BC，点C的坐标是__________．

    探究二：将线段OA绕点O逆时针旋转90°，设点A落在点D，则点D的坐标是__________；连接AD，则AD＝________(图②为备用图)．

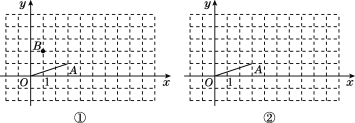
    (2)已知四点O(0，0)，A(a，b)，C，B(c，d)，顺次连接O，A，C，B，O，若所得到的四边形为平行四边形，则点C的坐标是____________．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，在梯形ABCD中，∠BCD=∠D=90，上底AD=3，下底BC=，高CD=4，沿AC把梯形ABCD翻折，点D是恰好落在AB边上的点E处，求△BCE面积。

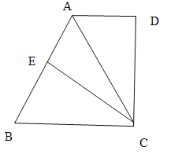
    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，点A和点B在数轴上对应的数分别为a和b，且（a+6）2+|b﹣8|＝0．

    （1）求线段AB的长；

    （2）点C在数轴上所对应的数为x，且x是方程x﹣1＝x+1的解，在线段AB上是否存在点D，使得AD+BD＝CD？若存在，请求出点D在数轴上所对应的数，若不存在，请说明理由；

    （3）在（2）的条件下，线段AD和BC分别以6个单位长度/秒和5个单位长度/秒的速度同时向右运动，运动时间为t秒，M为线段AD的中点，N为线段BC的中点，若MN＝12，求t的值．

    查看答案和解析>>

    同步练习册答案