
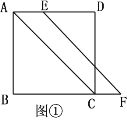
【题目】已知,在正方形ABCD中,点E在边AD上,点F在边BC的延长线上,且AE=CF,连接AC,EF.
(1)如图①,求证:EF//AC;
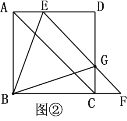
(2)如图②,EF与边CD交于点G,连接BG,BE,
①求证:△BAE≌△BCG;
②若BE=EG=4,求△BAE的面积.
【答案】(1)见解析;(2)①见解析;②△BAE的面积为2.
【解析】
(1)利用平行四边形的判定及其性质定理即可解决问题;
(2)①根据SAS可以证明两三角形全等;
②先根据等腰直角△DEG计算DE的长,设AE=a,表示正方形的边长,根据勾股定理列式,可得![]() +
+![]() a=4,最后根据三角形面积公式,整体代入可得结论.
a=4,最后根据三角形面积公式,整体代入可得结论.
(1)证明:∵正方形ABCD
∴AE//CF,
∵AE=CF
∴AEFC是平行四边形
∴EF//AC.
(2)①如图,
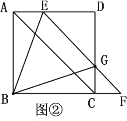
∵四边形ABCD是正方形,且EF∥AC,
∴∠DEG=∠DAC=45°,∠DGE=∠DCA=45°;
∵AD∥BF,
∴∠CFG=∠DEG=45°,
∵∠CGF=∠DGE=45°,
∴∠CGF=∠CFG,
∴CG=CF;
∵AE=CF,
∴AE=CG;
在△ABE与△CBG中,
∵AE=CG,∠BAE=∠BCG,AB=BC
∴△ABE≌CBG(SAS);
②由①知△DEG是等腰直角三角形,
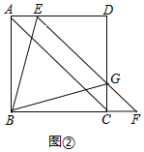
∵EG=4,
∴DE=![]() ,
,
设AE=a,则AB=AD=a+![]() ,
,
Rt△ABE中,由勾股定理得:AB2+AE2=BE2,
∴(a+![]() )2+a2=42,
)2+a2=42,
∴a2+![]() a=4,
a=4,
∴S△ABE=![]() ABAE=
ABAE=![]() a(a+
a(a+![]() )=
)=![]() (a2+
(a2+![]() a)=
a)=![]() ×4=2.
×4=2.


科目:初中数学 来源: 题型:
【题目】已知,如图:在△ABC中,AC=3,BC=6,∠C=60![]() ;
;
(1)将△ABC绕着点C旋转,使点A落在直线BC上的点A′,点B落在B′,在下图中画出旋转后的△A′B′C.
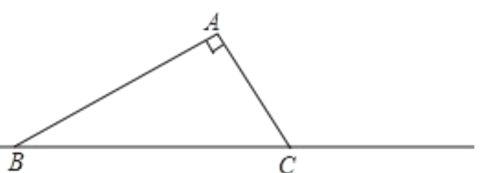
(2)直接写出A′B的长,A′B=___________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲、乙两位采购员同时去一家饲料公司买两次饲料,两次饲料的价格有变化,两位采购员的购货方式也不同,其中,甲每次购买1000千克,乙每次用去800元,而不管购买多少饲料,购买的饲料单价分别为m元/千克和n元/千克,
(1)甲、乙所购饲料的平均单价各是多少?
(2)谁的购货方式更合算?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小王同学在学校组织的社会调查活动中负责了解他所居住的小区450户居民的生活用水情况,他从中随机调查了50户居民的月均用水量(单位:t),并绘制了样本的频数分布表和频数分布直方图(如图).
月均用水量(单位:t) | 频数 | 百分比 |
2≤x<3 | 2 | 4% |
3≤x<4 | 12 | 24% |
4≤x<5 |
|
|
5≤x<6 | 10 | 20% |
6≤x<7 |
| 12% |
7≤x<8 | 3 | 6% |
8≤x<9 | 2 | 4% |
(1)请根据题中已有的信息补全频数分布表和频数分布直方图;
(2)如果家庭月均用水量“大于或等于4t且小于7t”为中等用水量家庭,请你估计总体小王所居住的小区中等用水量家庭大约有多少户?
(3)从月均用水量在2≤x<3,8≤x<9这两个范围内的样本家庭中任意抽取2个,请用列举法(画树状图或列表)求抽取出的2个家庭来自不同范围的概率.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知关于x的方程![]() =x+
=x+![]() 与
与![]() =6x﹣2的解互为倒数,
=6x﹣2的解互为倒数,
(1)求m的值.
(2)若当y=m时,代数式ay3+by+1的值为5,求当y=﹣m时,代数式ay3+by+1的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在四边形ABCD中,对角线AC平分∠DAB,∠ABD=52°,∠ABC=116°,∠ACB=α°,则∠BDC的度数为( )
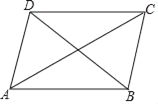
A. α B. ![]() C. 90﹣α D. 90﹣
C. 90﹣α D. 90﹣![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】计算:
(1)23﹣17﹣(﹣7)+(﹣16)
(2)![]()
(3)﹣22÷(﹣4)3+|0.8﹣1|×(2![]() )2
)2
(4)4xy+(3y2﹣2x2)﹣(5xy﹣2x2)﹣4y2
(5)先化简,再求值:![]() x﹣2(x﹣y2)+(﹣
x﹣2(x﹣y2)+(﹣![]() x+
x+![]() y2),其中x=﹣
y2),其中x=﹣![]() ,y=3
,y=3
查看答案和解析>>
科目:初中数学 来源: 题型:
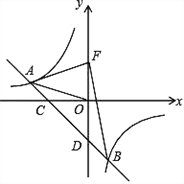
【题目】如图,一次函数 yax 2(a0) 的图象与反比例函数 y![]() (k0) 的图象交于 A、B两点,且与x轴、y轴分别交于点C、D.已知 tan∠AOC=
(k0) 的图象交于 A、B两点,且与x轴、y轴分别交于点C、D.已知 tan∠AOC=![]() ,AO=
,AO=![]() .
.
(1)求这个一次函数和反比例函数的解析式;
(2) 若点 F 是点D 关于 x 轴的对称点,求△ABF 的面积.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com