
【题目】如图(1),在□ABCD中,P是CD边上的一点,AP与BP分别平分∠DAB和∠CBA。
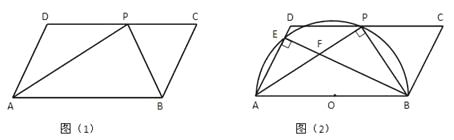
【1】判断△APB是什么三角形?证明你的结论;
【2】比较DP与PC的大小;
【3】如图(2)以AB为直径作半圆O,交AD于点E,连结BE与AP交于点F,若AD=5cm,AP=8cm,求证△AEF∽△APB,并求tan∠AFE的值。
【答案】
【1】 △APB是直角三角形,理由如下:
∵在□ABCD中,AD∥BC,
∴∠DAB +∠ABC = 180°;
又∵AP与BP分别平分∠DAB和∠CBA,
∴∠PAB =![]() ,∠PBA =
,∠PBA =![]() ,
,
∴∠PAB+∠PBA=![]() ,
,
∴△APB是直角三角形;
【2】 ∵DC∥AB,
∴∠BAP =∠DPA.
∵∠DAP =∠PAB,
∴∠DAP =∠DPA,
∴DA = DP
同理证得CP=CB.
∴DP = PC
【3】 ∵AB是⊙O直径,
∴∠AEB = 90°.
又(1)易知∠APB = 90°.
∴∠AEB =∠APB,
∵AP为角平分线,即∠EAF=∠PAB,
∴△AEF∽△APB,
由(2)可知DP =" PC" = AD,
∴ AB =" DC" =" 2AD" = 10cm,
在Rt△PAB中,![]() (cm)
(cm)
又△AEF∽△APB,
得∠AFE=∠ABP,
∴tan∠AFE = tan∠ABP=![]() 。
。
【解析】
【1】可通过角的度数来判断三角形APB的形状.由于ABCD是平行四边形,AD∥BC,那么同旁内角∠DAB和∠CBA的和应该是180°,AP,BE平分∠DAB,∠ABP,于是∠PAB和∠ABP的和就应该是90°,即∠APB=90°,因此可得出三角形APB的形状.
【2】可通过平行和角平分线,通过等角对等边得出DP=AP,同理可证出PC=BC,根据平行四边形的性质,AD=BC,可得出DP=PC.
【3】利用两个角相等求出△AEF∽△APB,然后利用(2)求出PB的长度,在根据∠AFE=∠ABP,然后求出tan∠AFE的值.


科目:初中数学 来源: 题型:
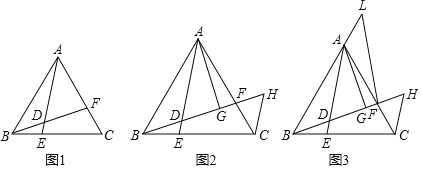
【题目】△ABC是等边三角形,点E、F分别是边BC、AC上的点,且BE=CF,AE、BF交于点D.
(1)如图1,求证:AE=BF.
(2)如图2,过点A作AG⊥BF于点G,过点C作CH∥AE交BF延长线于点H,若D为BG中点,求BH:CH的值;
(3)如图3,在(2)的条件下,L为BA延长线上一点,且FL=FB,△FLA的面积为2,求△ABC的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在⊙O的内接四边形ABCD中,AB=AD,∠C=120°,点E在⊙O上.
(1)求∠AED的度数;
(2)若⊙O的半径为2,则![]() 的长为多少?
的长为多少?
(3)连接OD,OE,当∠DOE=90°时,AE恰好是⊙O的内接正n边形的一边,求n的值.

查看答案和解析>>
科目:初中数学 来源: 题型:
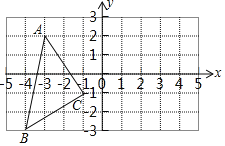
【题目】如图,在平面直角坐标系中,△ABC的顶点A、B、C坐标分别为(﹣3,2),(﹣4,﹣3),(﹣1,﹣1).
(1)画出△ABC关于y轴对称的△A1B1C1;(A、B、C的对称点分别为A1、B1、C1)
(2)写出△A1B1C1各顶点A1、B1、C1的坐标.A1 、B1 、C1
(3)直接写出△ABC的面积= .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小明在学习二次根式后,发现一些含根号的式子可以写成另一个式子的平方,如:3+2![]() ,善于思考的小明进行了以下探索:
,善于思考的小明进行了以下探索:
设a+b![]() (其中a、b、m、n均为整数),
(其中a、b、m、n均为整数),
则有:a+b![]() ,∴a=m2+2n2,b=2mn,这样小明就找到了一种把类似a+b
,∴a=m2+2n2,b=2mn,这样小明就找到了一种把类似a+b![]() 的式子化为平方式的方法.
的式子化为平方式的方法.
请你仿照小明的方法探索并解决下列问题:
(1)当a、b、m、n均为正整数时,若a+b![]() ,用含m、n的式子分别表示a、b得:a= ,b= ;
,用含m、n的式子分别表示a、b得:a= ,b= ;
(2)利用所探索的结论,用完全平方式表示出:7+4![]() = .
= .
(3)请化简:![]() .
.
查看答案和解析>>
科目:初中数学 来源: 题型:
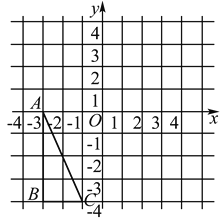
【题目】在平面直角坐标系中,△ABC的三个顶点坐标分别为A(-3,0),B(-3,-4),C(-1,-4).
(1)求△ABC的面积;
(2)在图中作出△ABC关于x轴对称的图形△DEF,点A、B、C的对称点分别为D、E、F,并写出D、E、F的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
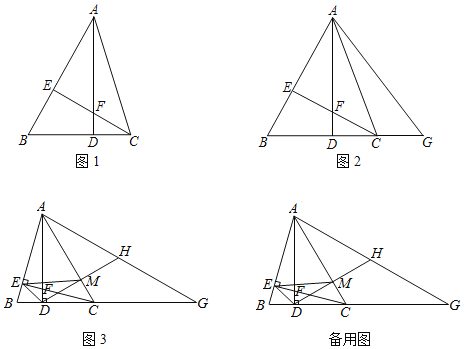
【题目】如图1,在△ABC中,AD⊥BC于D,CE⊥AB于E,AD与CE交于点F,∠ACE=45°.
(1)求证:BE=EF;
(2)如图2,G在BC的延长线上,连接GA,若GA=GB,求证:AC平分∠DAG;
(3)如图3,在(2)的条件下,H为AG的中点,连接DH交AC于M,连接EM、ED,若S△EMC=4,∠BAD=15°,求AM的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列说法正确的是( )
A.若 a、b、c是△ABC的三边,则a2+b2=c2
B.若 a、b、c是Rt△ABC的三边,则a2+b2=c2
C.若 a、b、c是Rt△ABC的三边,![]() ,则a2+b2=c2
,则a2+b2=c2
D.若 a、b、c是Rt△ABC的三边,![]() ,则a2+b2=c2
,则a2+b2=c2
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com