【题目】（10分）如图，已知△ABC为等边三角形，点D、E分别在BC、AC边上，且AE=CD，AD与BE相交于点F。
（1）求证：△ABE≌△CAD；（2）求∠BFD的度数。
【答案】（1）见解析；（2）60°
【解析】
试题分析：（1）根据等边三角形的性质可知∠BAC=∠C=60°，AB=CA，结合AE=CD，可证明△ABE≌△CAD，从而证得结论；
（2）根据∠BFD=∠ABE+∠BAD，∠ABE=∠CAD，可知∠BFD=∠CAD+∠BAD=∠BAC=60°．
试题解析：（1）证明：∵△ABC为等边三角形，
∴∠BAC=∠C=60°，AB=CA，
即∠BAE=∠C=60°，
在△ABE和△CAD中，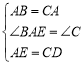
，
∴△ABE≌△CAD（SAS）。
（2）解：∵∠BFD=∠ABE+∠BAD，
又∵△ABE≌△CAD，
∴∠ABE=∠CAD．
∴∠BFD=∠CAD+∠BAD=∠BAC=60°．
科目：初中数学 来源： 题型：
【题目】如图，在△ABC中，∠ACB=90°，点D是AB上一点，以BD为直径的⊙O和AB相切于点P．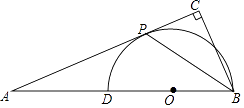
（1）求证：BP平分∠ABC；
（2）若PC=1，AP=3，求BC的长．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】在Rt△ABC中，∠C=90°，cosB=0.6，把这个直角三角形绕顶点C旋转后得到Rt△A'B'C，其中点B'正好落在AB上，A'B'与AC相交于点D，那么B′D：CD= ．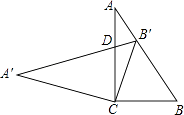 
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，在△ABC中，∠ABC=∠ACB，以AC为直径的⊙O分别交AB、BC于点M、N，点P在AB的延长线上，且∠CAB=2∠BCP．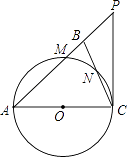
（1）求证：直线CP是⊙O的切线；
（2）若BC=2 
，sin∠BCP= 
，求⊙O的半径及△ACP的周长．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，点A、B、O是正方形网格上的三个格点，⊙O的半径为OA，点P是优弧 
上的一点，则cos∠APB的值是（ ）
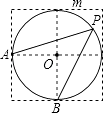
A.45°
B.1
C.
D.无法确定
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】二次函数y=ax2+bx+c的图象如图所示，则一次函数y=bx+b2﹣4ac与反比例函数y= 
在同一坐标系内的图象大致为（ ）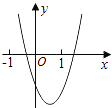
A.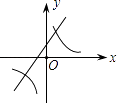
B.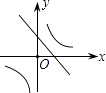
C.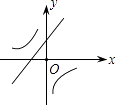
D.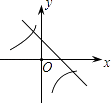
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
