
【题目】如图,已知A、B两点的坐标分别为(2,0)、(0,4),P是△AOB外接圆⊙C上的一点,且∠AOP=45°,则点P的坐标为________.
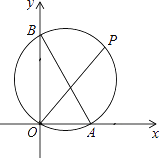
【答案】(3,3)
【解析】
由OA与OB的长,利用勾股定理求出AB的长,根据∠AOP=45°,得到三角形OPE为等腰直角三角形,即P横纵坐标相等,设为P(a,a),由∠AOB为直角,利用直角所对的弦为直径得到AB为直径,Rt△AOB外接圆的圆心为AB中点,求出圆心C坐标,过点C作CF∥OA,过点P作PE⊥OA于E交CF于F,在直角三角形PCF中,利用勾股定理列出关于a的方程,求出方程的解得到a的值,确定出P的坐标即可.
:
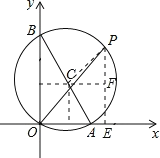 ∵OB=4,OA=2,
∵OB=4,OA=2,
∴AB=![]() =2
=2![]() ,
,
∵∠AOP=45°,
∴P点横纵坐标相等,可设为a,即P(a,a),
∵∠AOB=90°,
∴AB是直径,
∴Rt△AOB外接圆的圆心为AB中点,坐标C(1,2),
P点在圆上,P点到圆心的距离为圆的半径![]() ,
,
过点C作CF∥OA,过点P作PE⊥OA于E交CF于F,
∴∠CFP=90°,
∴PF=a2,CF=a1,PC=![]() ,
,
∴根据勾股定理得:(a2)2+(a1)2=(![]() )2,
)2,
解得:a=3,
∴P(3,3);
故答案为:(3,3).


 每日10分钟口算心算速算天天练系列答案
每日10分钟口算心算速算天天练系列答案科目:初中数学 来源: 题型:
【题目】某市每年都举行“希望杯”篮球赛,去年初赛阶段,共15支队伍参赛,每两队之间都比赛一场,下表是去年初赛部分队伍的积分榜.
队名 | 比赛场次 | 胜场 | 负场 | 积分 |
A | 14 | 10 | 4 | 24 |
B | 14 | 9 | 5 | 23 |
C | 14 | 4 | 10 | 18 |
D | 14 | 0 | 14 | 14 |
(1)去年某队的总积分为20分,则该队在比赛中胜了多少场?
(2)今年,参赛的队伍比去年有所增加,但因场地受限,组委会决定初赛阶段共安排40场比赛,并将参赛队伍平均分成4个小组,各小组每两队之间都比赛一场,求今年比去年增加了多少支队伍?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】计算:
(1)(2x2y)3(3x2y)
(2)(36x3-24x2+2x)÷4x
(3)(2x+y+1)(2x-y-1)
(4)(-3ax)2(5a2-3ax3)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“高低杠”是女子体操特有的一个竞技项目,其比赛器材由高、低两根平行杠及若干支架组成,运动员可根据自己的身高和习惯在规定范围内调节高、低两杠间的距离.某兴趣小组根据高低杠器材的一种截面图编制了如下数学问题,请你解答.
如图所示,底座上A,B两点间的距离为90cm.低杠上点C到直线AB的距离CE的长为155cm,高杠上点D到直线AB的距离DF的长为234cm,已知低杠的支架AC与直线AB的夹角∠CAE为82.4°,高杠的支架BD与直线AB的夹角∠DBF为80.3°.求高、低杠间的水平距离CH的长.(结果精确到1cm,参考数据sin82.4°≈0.991,cos82.4°≈0.132,tan82.4°≈7.500,sin80.3°≈0.983,cos80.3°≈0.168,tan80.3°≈5.850)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】寒梅中学为了丰富学生的课余生活,计划购买围棋和中国象棋供棋类兴趣小组活动使用,若购买3副围棋和5副中国象棋需用98元;若购买8副围棋和3副中国象棋需用158元;(1)求每副围棋和每副中国象棋各多少元;(2)寒梅中学决定购买围棋和中国象棋共40副,总费用不超过550元,那么寒梅中学最多可以购买多少副围棋?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】对角线长分别为6和8的菱形ABCD如图所示,点O为对角线的交点,过点O折叠菱形,使B,B′两点重合,MN是折痕.若B'M=1,则CN的长为( )
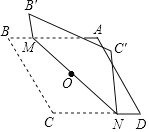
A. 7 B. 6 C. 5 D. 4
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com