
【题目】如图,在△ABC中,AB=AC,以AB为直径的⊙O交AC于点E,交BC于点D.求证:
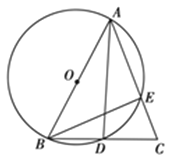
(1)D是BC的中点;
(2)△BEC∽△ADC.
科目:初中数学 来源: 题型:
【题目】如图,已知直线AC的表达式为y=![]() x+8,点P从点A开始沿AO向点O以1个单位/s的速度移动,点Q从点O开始沿OC向点C以2个单位/s的速度移动.如果P,Q两点分别从点A,O同时出发,经过几秒能使△PQO的面积为8个平方单位?
x+8,点P从点A开始沿AO向点O以1个单位/s的速度移动,点Q从点O开始沿OC向点C以2个单位/s的速度移动.如果P,Q两点分别从点A,O同时出发,经过几秒能使△PQO的面积为8个平方单位?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)如图①②,锐角的正弦值和余弦值都随着锐角的变化而变化.试探索随着锐角度数的增大,它的正弦值和余弦值变化的规律.
(2)根据你探索到的规律,试比较18°,34°,50°,62°,88°这些锐角的正弦值的大小和余弦值的大小.
(3)比较大小(在横线上填写“<”“>”或“=”):
若α=45°,则sin α cos α;
若α<45°,则sin α cos α;
若α>45°,则sin α cos α.
(4)利用互为余角的两个角的正弦和余弦的关系,试比较下列正弦值和余弦值的大小:sin 10°,cos 30°,sin 50°,cos 70°.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知A、B两点的坐标分别为(2,0)、(0,4),P是△AOB外接圆⊙C上的一点,且∠AOP=45°,则点P的坐标为________.
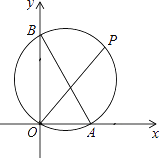
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知正方形ABCD中,BE平分∠DBC且交CD边于点E,将△BCE绕点C顺时针旋转到△DCF的位置,并延长BE交DF于点G.

(1)求证:△BDG∽△DEG;
(2)若EGBG=4,求BE的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点P在y轴的正半轴上,⊙P交x轴于B、C两点,以AC为直角边作等腰Rt△ACD,BD分别交y轴和⊙P于E、F两点,连接AC、FC.
(1)求证:∠ACF=∠ADB;
(2)若点A到BD的距离为m,BF+CF=n,求线段CD的长;
(3)当⊙P的大小发生变化而其他条件不变时,![]() 的值是否发生变化?若不发生变化,请求出其值;若发生变化,请说明理由.
的值是否发生变化?若不发生变化,请求出其值;若发生变化,请说明理由.
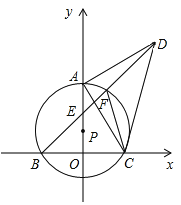
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AD是△ABC的边BC上的高,再添加下列条件中的某一个就能推出△ABC是等腰三角形.①BD=CD;②∠BAD=∠CAD;③AB+BD=AC+CD; ④AB-BD=AC-CD;⑤∠BAD=∠ACD.可以添加的条件序号正确答案是( )
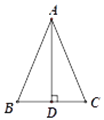
A.①②B.①②③C.①②③④D.①②③④⑤.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知关于![]() 的代数式
的代数式![]() ,设代数式
,设代数式![]() 的值
的值![]() .
.
下表中列出了当![]() 分别取-1,0,1,2,3,4,5,…,
分别取-1,0,1,2,3,4,5,…,![]() ,
,![]() ,…时对应的
,…时对应的![]() 值.
值.
| … | -1 | 0 | 1 | 2 | 3 | 4 | 5 | … |
|
| … |
| … | 10 | 5 | 2 | 1 | 2 | 5 |
| … |
|
| … |
(1)表中![]() 的值为 ;
的值为 ;
(2)当![]() 时,
时,![]() 有最小值,最小值是 ;
有最小值,最小值是 ;
(3)比较![]() 与
与![]() 的大小.
的大小.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com