
【题目】如图,AD是△ABC的边BC上的高,再添加下列条件中的某一个就能推出△ABC是等腰三角形.①BD=CD;②∠BAD=∠CAD;③AB+BD=AC+CD; ④AB-BD=AC-CD;⑤∠BAD=∠ACD.可以添加的条件序号正确答案是( )
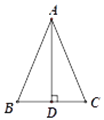
A.①②B.①②③C.①②③④D.①②③④⑤.
【答案】C
【解析】
可根据等腰三角形三线合一的性质来判断①②⑤是否正确;③④要通过作等腰三角形来判断其结论是否成立.
①∵AD⊥BC,BD=CD,
∴AD是BC的垂直平分线,
∴△ABC是等腰三角形;
故①正确;
②当∠BAD=∠CAD时,
∵AD是∠BAC的平分线,且AD是BC边上的高;
则△ABD≌△ACD,
∴△BAC是等腰三角形;
故②正确;
③延长DB至E,使BE=AB;延长DC至F,使CF=AC;连接AE、AF;
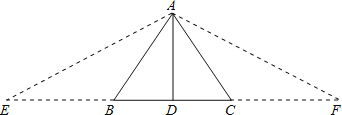
∵AB+BD=CD+AC,
∴DE=DF,又AD⊥BC;
∴△AEF是等腰三角形;
∴∠E=∠F;
∵AB=BE,
∴∠ABC=2∠E;
同理,得∠ACB=2∠F;
∴∠ABC=∠ACB,即AB=AC,△ABC是等腰三角形;
故③正确;
④△ABC中,AD⊥BC,根据勾股定理,得:
AB2-BD2=AC2-CD2,
即(AB+BD)(AB-BD)=(AC+CD)(AC-CD);
∵AB-BD=AC-CD(1),
∴AB+BD=AC+CD(2);
∴(1)+(2)得:,
2AB=2AC;
∴AB=AC,
∴△ABC是等腰三角形;
故④正确;
⑤无法判定;
故⑤错误.
正确的是①②③④.
故选C.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
【题目】如图1,CA=CB,CD=CE,∠ACB=∠DCE=α.
(1)求证:BE=AD;

(2)当α=90°时,取AD,BE的中点分别为点P、Q,连接CP,CQ,PQ,如图②,判断△CPQ的形状,并加以证明.

查看答案和解析>>
科目:初中数学 来源: 题型:
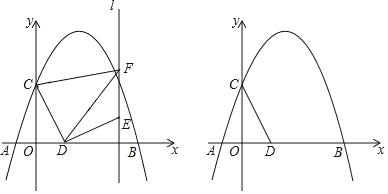
【题目】如图,抛物线y=﹣![]() +bx+c交x轴于点A(﹣2,0)和点B,交y轴于点C(0,3),点D是x轴上一动点,连接CD,将线段CD绕点D旋转得到DE,过点E作直线l⊥x轴,垂足为H,过点C作CF⊥l于F,连接DF.
+bx+c交x轴于点A(﹣2,0)和点B,交y轴于点C(0,3),点D是x轴上一动点,连接CD,将线段CD绕点D旋转得到DE,过点E作直线l⊥x轴,垂足为H,过点C作CF⊥l于F,连接DF.
(1)求抛物线解析式;
(2)若线段DE是CD绕点D顺时针旋转90°得到,求线段DF的长;
(3)若线段DE是CD绕点D旋转90°得到,且点E恰好在抛物线上,请求出点E的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知AB=AC,AD=AE,若添加一个条件不能得到“△ABD≌△ACE”是( )
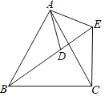
A. ∠ABD=∠ACE B. BD=CE C. ∠BAD=∠CAE D. ∠BAC=∠DAE
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了维护国家主权和海洋权力,海监部门对我国领海实现了常态化巡航管理,如图,正在执行巡航任务的海监船以每小时50海里的速度向正东方航行,在![]() 处测得灯塔
处测得灯塔![]() 在北偏东
在北偏东![]() 方向上,继续航行1小时到达
方向上,继续航行1小时到达![]() 处,此时测得灯塔
处,此时测得灯塔![]() 在北偏东
在北偏东![]() 方向上.
方向上.
(1)求![]() 的度数;
的度数;
(2)已知在灯塔![]() 的周围25海里内有暗礁,问海监船继续向正东方向航行是否安全?
的周围25海里内有暗礁,问海监船继续向正东方向航行是否安全?

查看答案和解析>>
科目:初中数学 来源: 题型:
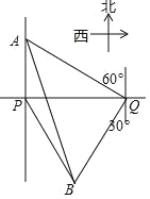
【题目】一轮船在P处测得灯塔A在正北方向,灯塔B在南偏东30°方向,轮船向正东航行了900m,到达Q处,测得A位于北偏西60°方向, B位于南偏西30°方向.
(1)线段BQ与PQ是否相等?请说明理由;
(2)求A、B间的距离(结果保留根号).
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com