
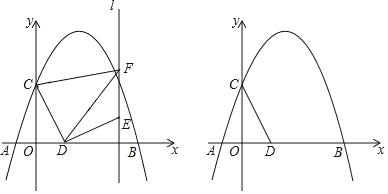
【题目】如图,抛物线y=﹣![]() +bx+c交x轴于点A(﹣2,0)和点B,交y轴于点C(0,3),点D是x轴上一动点,连接CD,将线段CD绕点D旋转得到DE,过点E作直线l⊥x轴,垂足为H,过点C作CF⊥l于F,连接DF.
+bx+c交x轴于点A(﹣2,0)和点B,交y轴于点C(0,3),点D是x轴上一动点,连接CD,将线段CD绕点D旋转得到DE,过点E作直线l⊥x轴,垂足为H,过点C作CF⊥l于F,连接DF.
(1)求抛物线解析式;
(2)若线段DE是CD绕点D顺时针旋转90°得到,求线段DF的长;
(3)若线段DE是CD绕点D旋转90°得到,且点E恰好在抛物线上,请求出点E的坐标.
【答案】(1) 抛物线解析式为y=﹣![]() ;(2) DF=3
;(2) DF=3![]() ;(3) 点E的坐标为E1(4,1)或E2(﹣
;(3) 点E的坐标为E1(4,1)或E2(﹣![]() ,﹣
,﹣![]() )或E3(
)或E3(![]() ,﹣
,﹣![]() )或E4(
)或E4(![]() ,﹣
,﹣![]() ).
).
【解析】
(1)将点A、C坐标代入抛物线解析式求解可得;
(2)证△COD≌△DHE得DH=OC,由CF⊥FH知四边形OHFC是矩形,据此可得FH=OC=DH=3,利用勾股定理即可得出答案;
(3)设点D的坐标为(t,0),由(1)知△COD≌△DHE得DH=OC、EH=OD,再分CD绕点D顺时针旋转和逆时针旋转两种情况,表示出点E的坐标,代入抛物线求得t的值,从而得出答案.
(1)∵抛物线y=﹣![]() +bx+c交x轴于点A(﹣2,0)、C(0,3),∴
+bx+c交x轴于点A(﹣2,0)、C(0,3),∴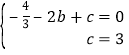 ,解得:
,解得:![]() ,∴抛物线解析式为y=﹣
,∴抛物线解析式为y=﹣![]() +
+![]() x+3;
x+3;
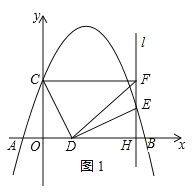
(2)如图1.
∵∠CDE=90°,∠COD=∠DHE=90°,∴∠OCD+∠ODC=∠HDE+∠ODC,∴∠OCD=∠HDE.
又∵DC=DE,∴△COD≌△DHE,∴DH=OC.
又∵CF⊥FH,∴四边形OHFC是矩形,∴FH=OC=DH=3,∴DF=3![]() ;
;
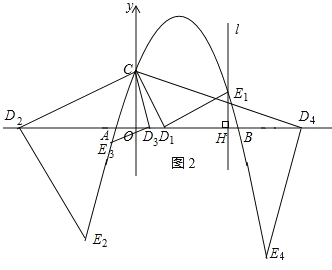
(3)如图2,设点D的坐标为(t,0).
∵点E恰好在抛物线上,且EH=OD,∠DHE=90°,∴由(2)知,△COD≌△DHE,∴DH=OC,EH=OD,分两种情况讨论:
①当CD绕点D顺时针旋转时,点E的坐标为(t+3,t),代入抛物线y=﹣![]() +
+![]() x+3,得:﹣
x+3,得:﹣![]() (t+3)2+
(t+3)2+![]() (t+3)+3=t,解得:t=1或t=﹣
(t+3)+3=t,解得:t=1或t=﹣![]() ,所以点E的坐标E1(4,1)或E2(﹣
,所以点E的坐标E1(4,1)或E2(﹣![]() ,﹣
,﹣![]() );
);
②当CD绕点D逆时针旋转时,点E的坐标为(t﹣3,﹣t),代入抛物线y=﹣![]() +
+![]() x+3得:﹣
x+3得:﹣![]() (t﹣3)2+
(t﹣3)2+![]() (t﹣3)+3=﹣t,解得:t=
(t﹣3)+3=﹣t,解得:t=![]() 或t=
或t=![]() .故点E的坐标E3(
.故点E的坐标E3(![]() ,﹣
,﹣![]() )或E4(
)或E4(![]() ,﹣
,﹣![]() );
);
综上所述:点E的坐标为E1(4,1)或E2(﹣![]() ,﹣
,﹣![]() )或E3(
)或E3(![]() ,﹣
,﹣![]() )或E4(
)或E4(![]() ,﹣
,﹣![]() ).
).


科目:初中数学 来源: 题型:
【题目】在如图所示的直角坐标系中,解答下列问题.
(1)分别写出A、B两点的坐标:A ,B .
(2)△ABC的面积= ;点B到AC的距离= .
(3)画出△ABC关于x轴对称的△A1B1C1.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知半圆![]() 的直径
的直径![]() ,在
,在![]() 中,
中,![]() ,
,![]() ,
,![]() ,半圆
,半圆![]() 以
以![]() 的速度从左向右运动,在运动过程中,点
的速度从左向右运动,在运动过程中,点![]() 、
、![]() 始终在直线
始终在直线![]() 上.设运动时间为
上.设运动时间为![]() ,当
,当![]() 时,半圆
时,半圆![]() 在
在![]() 的左侧,
的左侧,![]() .
.
![]() 当
当![]() 为何值时,
为何值时,![]() 的一边所在直线与半圆
的一边所在直线与半圆![]() 所在的圆相切?
所在的圆相切?
![]() 当
当![]() 的一边所在直线与半圆
的一边所在直线与半圆![]() 所在的圆相切时,如果半圆
所在的圆相切时,如果半圆![]() 与直线
与直线![]() 围成的区域与
围成的区域与![]() 三边围成的区域有重叠部分,求重叠部分的面积.
三边围成的区域有重叠部分,求重叠部分的面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知AB∥CD,F为CD上一点,∠EFD=60°,∠AEC=2∠CEF,若6°<∠BAE<15°,∠C的度数为整数,则∠C的度数为_____.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AD是BC边上的高,AE是∠BAC的平分线,∠EAD=15°,∠B=40°.
(1)求∠C的度数.
(2)若:∠EAD=α,∠B=β,其余条件不变,直接写出用含α,β的式子表示∠C的度数.

查看答案和解析>>
科目:初中数学 来源: 题型:
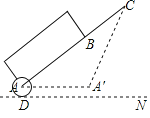
【题目】拉杆箱是人们出行的常用品,采用拉杆箱可以让人们出行更轻松.如图,一直某种拉杆箱箱体长AB=65cm,拉杆最大伸长距离BC=35cm,在箱体底端装有一圆形滚轮,当拉杆拉到最长时,滚轮的圆心在图中的A处,点A到地面的距离AD=3cm,当拉杆全部缩进箱体时,滚轮圆心水平向右平移55cm到A′处,求拉杆把手C离地面的距离(假设C点的位置保持不变).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知函数y=x2﹣2mx+2016(m为常教)的图象上有三点:A(x1,y1)、B(x2,y2)、C(x3,y3),其中x1=![]() +m,x2=
+m,x2=![]() +m,x3=m﹣1,则y1、y2、y3的大小关系是( )
+m,x3=m﹣1,则y1、y2、y3的大小关系是( )
A. y2<y3<y1 B. y3<y1<y2 C. y1<y2<y3 D. y1<y3<y2
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某公司生产某种产品的成本是200元/件,售价是250元/件,年销售量为10万件.为了获得更好的效益,公司准备拿出一定的资金做广告.根据经验,每年投入的广告费用x万元,产品的年销售量将是原销售量的y倍,且y与x之间满足二次函数关系:y=﹣0.001x2+0.06x+1.
(1)如果把利润看作是销售总额减去成本费用和广告费用,试求出年利润S(万元)与广告费用x(万元)的函数关系式(无需自变量的取值范围);
(2)如果公司年投入的广告费不低于10万元且不高于50万元,求年利润S的最大值;
(3)若公司希望年利润在776万元到908万元之间(含端点),请从节约支出的角度直接写出广告费x的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知直角△ABC,∠BAC=90°,D是斜边BC的中点,E、F分别是AB、AC边上的点,且DE⊥DF连接EF

(1)如图1,求证:∠BED=∠AFD;
(2)求证:BE2+CF2=EF2;
(3)如图2,当∠ABC=45°,若BE=12,CF=5,求△DEF的面积.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com