【题目】如图，已知AB∥CD，F为CD上一点，∠EFD=60°，∠AEC=2∠CEF，若6°＜∠BAE＜15°，∠C的度数为整数，则∠C的度数为_____．
【答案】36°或37°．
【解析】分析：先过E作EG∥AB，根据平行线的性质可得∠AEF=∠BAE+∠DFE，再设∠CEF=x，则∠AEC=2x，根据6°＜∠BAE＜15°，即可得到6°＜3x-60°＜15°，解得22°＜x＜25°，进而得到∠C的度数．
详解：如图，过E作EG∥AB，
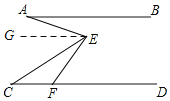
∵AB∥CD，
∴GE∥CD，
∴∠BAE=∠AEG，∠DFE=∠GEF，
∴∠AEF=∠BAE+∠DFE，
设∠CEF=x，则∠AEC=2x，
∴x+2x=∠BAE+60°，
∴∠BAE=3x-60°，
又∵6°＜∠BAE＜15°，
∴6°＜3x-60°＜15°，
解得22°＜x＜25°，
又∵∠DFE是△CEF的外角，∠C的度数为整数，
∴∠C=60°-23°=37°或∠C=60°-24°=36°，
故答案为：36°或37°．
发散思维新课堂系列答案科目：初中数学 来源： 题型：
【题目】已知分式
．
（1）当____时，分式的值等于零；
（2）当____时，分式无意义；
（3）当___且___时分式的值是正数；
（4）当____时，分式的值是负数．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】我们用[a]表示不大于a的最大整数，例如：[2.5]＝2，[3]＝3，[－2.5]＝－3；用<a>表示大于a的最小整数，例如：<2.5>＝3，<4>＝5，<－1.5>＝－1.
解决下列问题：
（1）[－4.5]＝___，<3.5>＝___；
（2）若[x]＝2，则x的取值范围是___；若<y>＝－1，则y的取值范围是___.
（3）已知x，y满足方程组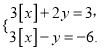
求x，y的取值范围.
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，矩形ABCD中，AB=4，BC=2，E是AB的中点，直线l平行于直线EC，且直线l与直线EC之间的距离为2，点F在矩形ABCD边上，将矩形ABCD沿直线EF折叠，使点A恰好落在直线l上，则DF的长为 ． 
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】画出函数
的图象.
（1）函数
的自变量x的取值范围是________；
（2）列表（把表格补充完整）
x | …… | -2 | -1 | 0 | 1 | 2 | 3 | 4 | …… |
y |
（3）描点、连线
（4）结合图象，写出函数的一条性质________________________________________.
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】2018年体育中考在即，学校体育组对九（1）班50名学生进行了长跑项目的测试，根据测试成绩制作了如图两个统计图．
根据统计图解答下列问题：
（1）本次测试的学生中，得4分的学生有多少人？
（2）本次测试的平均分是多少？
（3）通过一段时间的训练，体育组对该班学生的长跑项目进行第二次测试，测得成绩的最低分为3分，且得4分和5分的人数共有45人，平均分比第一次提高了0.8分，问第二次测试中，得4分、5分的学生分别有多少人？
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】为了推进我市校园体育运动的发展，2017年义乌市中小学运动会在雪峰中学成功举办．在此期间，某体育文化用品商店计划一次性购进篮球和排球共60个，其进价与售价间的关系如下表：
篮球 | 排球 | |
进价（元/个） | 80 | 50 |
售价（元/个） | 105 | 70 |
（1）商店用4200元购进这批篮球和排球，求购进篮球和排球各多少个？
（2）设商店所获利润为y（单位：元），购进篮球的个数为x（单位：个），请写出y与x之间的函数关系式（不要求写出x的取值范围）；
（3）若要使商店的进货成本在4300元的限额内，且全部销售完后所获利润不低于1400元，请你列举出商店所有进货方案，并求出最大利润是多少？
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，AC⊥x轴于点A，点B在y轴的正半轴上，∠ABC=60°，AB=4，BC=
，点D为AC与反比例函数
的图象的交点．若直线BD将△ABC的面积分成1：2的两部分，则k的值为______．
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com