
【题目】某公司生产某种产品的成本是200元/件,售价是250元/件,年销售量为10万件.为了获得更好的效益,公司准备拿出一定的资金做广告.根据经验,每年投入的广告费用x万元,产品的年销售量将是原销售量的y倍,且y与x之间满足二次函数关系:y=﹣0.001x2+0.06x+1.
(1)如果把利润看作是销售总额减去成本费用和广告费用,试求出年利润S(万元)与广告费用x(万元)的函数关系式(无需自变量的取值范围);
(2)如果公司年投入的广告费不低于10万元且不高于50万元,求年利润S的最大值;
(3)若公司希望年利润在776万元到908万元之间(含端点),请从节约支出的角度直接写出广告费x的取值范围.
【答案】(1)S═﹣![]() x2+29x+500(2)年利润S的最大920.5(3)从节约支出的角度直接写出广告费x的取值范围为12≤x≤24
x2+29x+500(2)年利润S的最大920.5(3)从节约支出的角度直接写出广告费x的取值范围为12≤x≤24
【解析】
(1)根据利润=(销售单价-成本)×销售量-广告费用,列出函数关系式,化简成一般式即可得;
(2)将(1)中二次函数一般式配方成二次函数的顶点式,由x的范围结合二次函数的性质即可得;
(3)若公司希望年利润在776万元到908万元之间,则有776≤s≤908,据此列不等式求解即可.
(1)S=(250﹣200)10y﹣x=﹣![]() x2+29x+500,
x2+29x+500,
答:年利润S(万元)与广告费用x(万元)的函数关系式S═﹣![]() x2+29x+500,
x2+29x+500,
(2)∵S=﹣![]() (x﹣29)2+920.5(10≤x≤50),
(x﹣29)2+920.5(10≤x≤50),
∴当10≤x<29时,S随着x的增大而增大
当29<x≤50时,S随着x的增大而减小
当S=29时,S有最大值为920.5.
年利润S的最大920.5.
(3)若公司希望年利润在776万元到908万元之间,即:776≤s≤908,
则:776≤﹣![]() x2+29x+500≤908,
x2+29x+500≤908,
由于x<29时,S随着x的增大而增大,而最大利润是920.5,所以,x<29,
解上述不等式得:12≤x≤24.
答:从节约支出的角度直接写出广告费x的取值范围为12≤x≤24.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
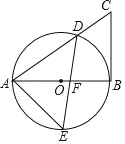
【题目】如图,AB是⊙O的直径,弦DE交AB于点F,⊙O的切线BC与AD的延长线交于点C,连接AE.
(1)试判断∠AED与∠C的数量关系,并说明理由;
(2)若AD=3,∠C=60°,点E是半圆AB的中点,则线段AE的长为 .
查看答案和解析>>
科目:初中数学 来源: 题型:
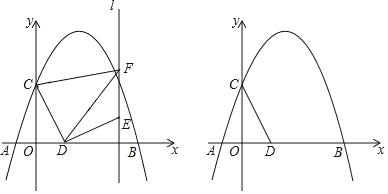
【题目】如图,抛物线y=﹣![]() +bx+c交x轴于点A(﹣2,0)和点B,交y轴于点C(0,3),点D是x轴上一动点,连接CD,将线段CD绕点D旋转得到DE,过点E作直线l⊥x轴,垂足为H,过点C作CF⊥l于F,连接DF.
+bx+c交x轴于点A(﹣2,0)和点B,交y轴于点C(0,3),点D是x轴上一动点,连接CD,将线段CD绕点D旋转得到DE,过点E作直线l⊥x轴,垂足为H,过点C作CF⊥l于F,连接DF.
(1)求抛物线解析式;
(2)若线段DE是CD绕点D顺时针旋转90°得到,求线段DF的长;
(3)若线段DE是CD绕点D旋转90°得到,且点E恰好在抛物线上,请求出点E的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】定义:如图(1),若分别以△ABC的三边AC、BC、AB为边向三角形外侧作正方形ACDE、BCFG和ABMN,则称这三个正方形为△ABC的外展三叶正方形,其中任意两个正方形为△ABC的外展
双叶正方形.
(1)作△ABC的外展双叶正方形ACDE和BCFG,记△ABC,△DCF的面积分别为S1和S2.
①如图(2),当∠ACB=90°时,求证:S1=S2;
②如图(3),当∠ACB≠90°时,S1与S2是否仍然相等,请说明理由.
(2)已知△ABC中,AC=3,BC=4,作其外展三叶正方形,记△DCF、△AEN、△BGM的面积和为S,请利用图(1)探究:当∠ACB的度数发生变化时,S的值是否发生变化?若不变,求出S的值;若变化,求出S的最大值.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】王师傅承包了一片池塘养水产品,他用总长为88m的围网围成如图所示的5个区域,其中②③④⑤四个区域面积相等.设AH=xm,整个矩形区域的面积为ym2.
(1)求y与x之间的函数关系式,并注明自变量x的取值范围;
(2)当x为何值时,y取最大值?最大值是多少?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在![]() 中,
中,![]() 、
、![]() 、
、![]() 三边的长分别为
三边的长分别为![]() 、
、![]() 、
、![]() ,求这个三角形的面积.小辉同学在解答这道题时,先建立一个正方形网格(每个小正方形的边长为1),再在网格中画出格点
,求这个三角形的面积.小辉同学在解答这道题时,先建立一个正方形网格(每个小正方形的边长为1),再在网格中画出格点![]() (即
(即![]() 三个顶点都在小正方形的顶点处),如图①所示.这样不需求
三个顶点都在小正方形的顶点处),如图①所示.这样不需求![]() 的高,而借用网格就能计算出它的面积.
的高,而借用网格就能计算出它的面积.
(1)请你将![]() 的面积直接填写在横线上.__________________
的面积直接填写在横线上.__________________
(2)我们把上述求![]() 面积的方法叫做构图法.若
面积的方法叫做构图法.若![]() 三边的长分别为
三边的长分别为![]() 、
、![]() 、
、![]() (
(![]() ),请利用图②的正方形网格(每个小正方形的边长为
),请利用图②的正方形网格(每个小正方形的边长为![]() )画出相应的
)画出相应的![]() ,并求出它的面积.
,并求出它的面积.
(3) 若△ABC三边的长分别为![]() 、
、![]() 、
、![]() (m>0,n>0,且m≠n),请利用图③的长方形网格试运用构图法求出这三角形的面积.
(m>0,n>0,且m≠n),请利用图③的长方形网格试运用构图法求出这三角形的面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】随着人们经济收入的不断提高,汽车已越来越多地进入到各个家庭.某大型超市为缓解停车难问题,建筑设计师提供了楼顶停车场的设计示意图.按规定,停车场坡道口上坡要张贴限高标志,以便告知车辆能否安全驶入.如图,地面所在的直线ME与楼顶所在的直线AC是平行的,CD的厚度为0.5m,求出汽车通过坡道口的限高DF的长(结果精确到0.1m,sin28°≈0.47,cos28°≈0.88,tan28°≈0.53).

查看答案和解析>>
科目:初中数学 来源: 题型:
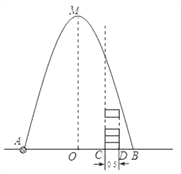
【题目】如图,在水平地面点A处有一网球发射器向空中发射网球,网球飞行路线是一条抛物线,在地面上落点为B,有人在直线AB上点C(靠点B一侧)竖直向上摆放若干个无盖的圆柱形桶.试图让网球落入桶内,已知AB=4米,AC=3米,网球飞行最大高度OM=5米,圆柱形桶的直径为0.5米,高为0.3米(网球的体积和圆柱形桶的厚度忽略不计).当竖直摆放圆柱形桶至少________个时,网球可以落入桶内.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com