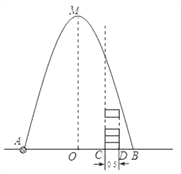
【题目】如图，在水平地面点A处有一网球发射器向空中发射网球，网球飞行路线是一条抛物线，在地面上落点为B，有人在直线AB上点C（靠点B一侧）竖直向上摆放若干个无盖的圆柱形桶．试图让网球落入桶内，已知AB=4米，AC=3米，网球飞行最大高度OM=5米，圆柱形桶的直径为0.5米，高为0.3米（网球的体积和圆柱形桶的厚度忽略不计）．当竖直摆放圆柱形桶至少________个时，网球可以落入桶内．

参考答案：

【答案】8

【解析】以点O为原点，AB所在直线为x轴建立直角坐标系（如图），

M（0，5），B（2，0），C（1，0），D（，0）,

设抛物线的解析式为y=ax2+k，

抛物线过点M和点B，

则k=5，a=﹣ ,

∴抛物线解析式为：y=﹣x2+5；

∴当x=1时，y=；

当x=时，y= ,

∴P（1， ），Q（， ）在抛物线上；

设竖直摆放圆柱形桶m个时网球可以落入桶内，

由题意，得， ≤m≤，

解得：7≤m≤12；

∵m为整数，

∴m的最小整数值为：8，

∴竖直摆放圆柱形桶至少8个时，网球可以落入桶内,

故答案为：8．

关闭