
【题目】如图是一个横断面为抛物线形状的拱桥,当水面宽![]() 米时,拱顶(拱桥洞的最高点)离水面
米时,拱顶(拱桥洞的最高点)离水面![]() ,水面上升
,水面上升![]() 时,水面的宽度为________.
时,水面的宽度为________.

【答案】![]()
【解析】
根据已知得出直角坐标系,进而求出二次函数解析式,再通过把y=1代入抛物线解析式得出水面宽度,即可得出答案.
建立平面直角坐标系,设横轴x通过AB,纵轴y通过AB中点O且通过C点,则通过画图可得知O为原点,
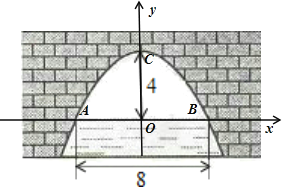
抛物线以y轴为对称轴,且经过A,B两点,OA和OB可求出为AB的一半4米,抛物线顶点C坐标为(0,4),
通过以上条件可设顶点式y=ax2+4,其中a可通过代入A点坐标(-4,0)到抛物线解析式得出:a=-![]() ,
,
所以抛物线解析式为y=-![]() x2+4,
x2+4,
当水面上升1米,通过抛物线在图上的观察可转化为:
当y=1时,对应的抛物线上两点之间的距离,也就是直线y=1与抛物线相交的两点之间的距离,
可以通过把y=1代入抛物线解析式得出:
1=-![]() x2+4,
x2+4,
解得:x=±2![]() ,
,
所以水面宽度增加到4![]() 米,
米,
故答案为:4![]() .
.


 小题狂做系列答案
小题狂做系列答案科目:初中数学 来源: 题型:
【题目】王师傅承包了一片池塘养水产品,他用总长为88m的围网围成如图所示的5个区域,其中②③④⑤四个区域面积相等.设AH=xm,整个矩形区域的面积为ym2.
(1)求y与x之间的函数关系式,并注明自变量x的取值范围;
(2)当x为何值时,y取最大值?最大值是多少?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在一个三角形中,如果一个角是另一个角的2倍,我们称这种三角形为倍角三角形.如图1,倍角△ABC中,∠A=2∠B,∠A、∠B、∠C的对边分别记为a,b,c,倍角三角形的三边a,b,c有什么关系呢?让我们一起来探索.

(1)我们先从特殊的倍角三角形入手研究.请你结合图形填空:
三三角形角形 | 角的已知量 |
|
|
图2 | ∠A=2∠B=90° | ||
图3 | ∠A=2∠B=60° |
(2)如图4,对于一般的倍角△ABC,若∠CAB=2∠CBA,∠CAB、∠CBA、∠C的对边分别记为a,b,c,a,b,c,三边有什么关系呢?请你作出猜测,并结合图4给出的辅助线提示加以证明;
(3)请你运用(2)中的结论解决下列问题:若一个倍角三角形的两边长为5,6,求第三边长.(直接写出结论即可)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知关于x的一元二次方程![]() 有实数根.
有实数根.
(1)求m的值;
(2)先作![]() 的图象关于x轴的对称图形,然后将所作图形向左平移3个单位长度,再向上平移2个单位长度,写出变化后图象的解析式;
的图象关于x轴的对称图形,然后将所作图形向左平移3个单位长度,再向上平移2个单位长度,写出变化后图象的解析式;
(3)在(2)的条件下,当直线y=2x+n(n≥m)与变化后的图象有公共点时,求![]() 的最大值和最小值.
的最大值和最小值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,![]() 为等腰三角形,顶点
为等腰三角形,顶点 ![]() 的坐标为
的坐标为 ![]() ,底边
,底边 ![]() 在
在 ![]() 轴上.将
轴上.将 ![]() 绕点
绕点 ![]() 按顺时针方向旋转一定角度后得
按顺时针方向旋转一定角度后得 ![]() ,点
,点 ![]() 的对应点
的对应点 ![]() 在
在 ![]() 轴上,那么点
轴上,那么点 ![]() 的横坐标是( )
的横坐标是( )

A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在水平地面点A处有一网球发射器向空中发射网球,网球飞行路线是一条抛物线,在地面上落点为B,有人在直线AB上点C(靠点B一侧)竖直向上摆放若干个无盖的圆柱形桶.试图让网球落入桶内,已知AB=4米,AC=3米,网球飞行最大高度OM=5米,圆柱形桶的直径为0.5米,高为0.3米(网球的体积和圆柱形桶的厚度忽略不计).当竖直摆放圆柱形桶至少________个时,网球可以落入桶内.
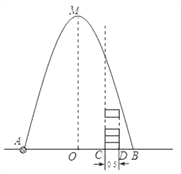
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】大学毕业生小王响应国家“自主创业”的号召,利用银行小额无息贷款开办了一家饰品店.该店购进一种今年新上市的饰品进行销售,饰品的进价为每件![]() 元,售价为每件
元,售价为每件![]() 元,每月可卖出
元,每月可卖出![]() 件.市场调查反映:调整价格时,售价每涨
件.市场调查反映:调整价格时,售价每涨![]() 元每月要少卖
元每月要少卖![]() 件;售价每下降
件;售价每下降![]() 元每月要多卖
元每月要多卖![]() 件.为了获得更大的利润,现将饰品售价调整为
件.为了获得更大的利润,现将饰品售价调整为![]() (元/件)(
(元/件)(![]() 即售价上涨,
即售价上涨,![]() 即售价下降),每月饰品销量为
即售价下降),每月饰品销量为![]() (件),月利润为
(件),月利润为![]() (元).
(元).
![]() 直接写出
直接写出![]() 与
与![]() 之间的函数关系式;
之间的函数关系式;
![]() 如何确定销售价格才能使月利润最大?求最大月利润;
如何确定销售价格才能使月利润最大?求最大月利润;
![]() 为了使每月利润不少于
为了使每月利润不少于![]() 元应如何控制销售价格?
元应如何控制销售价格?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,已知点![]() ,
,![]() 与坐标原点O在同一直线上,且AO=BO,其中m,n满足
与坐标原点O在同一直线上,且AO=BO,其中m,n满足![]() .
.
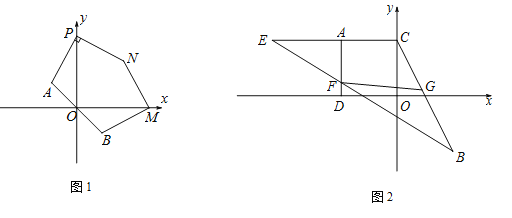
(1)求点A,B的坐标;
(2)如图1,若点M,P分别是x轴正半轴和y轴正半轴上的点,点P的纵坐标不等于2,点N在第一象限内,且![]() ,PA⊥PN,
,PA⊥PN,![]() ,求证:BM⊥MN;
,求证:BM⊥MN;
(3)如图2,作AC⊥y轴于点C,AD⊥x轴于点D,在CA延长线上取一点E,使![]() ,连结BE交AD于点F,恰好有
,连结BE交AD于点F,恰好有![]() ,点G是CB上一点,且
,点G是CB上一点,且![]() ,连结FG,求证:
,连结FG,求证:![]() .
.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AD是△ABC的高线,BD=CD,点E是AD上一点,BE=BC,将△ABE沿BE所在直线折叠,点A落在点A′位置上,连接AA',BA′,EA′与AC相交于点H,BA′与AC相交于点F.小夏依据上述条件,写出下列四个结论:①∠EBC=60°;②∠BFC=60°;③∠EA′A=60°;④∠A′HA=60°.以上结论中,正确的是( )

A.①B.③④C.①②③D.①②④
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com