
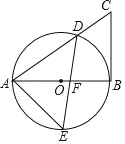
【题目】如图,AB是⊙O的直径,弦DE交AB于点F,⊙O的切线BC与AD的延长线交于点C,连接AE.
(1)试判断∠AED与∠C的数量关系,并说明理由;
(2)若AD=3,∠C=60°,点E是半圆AB的中点,则线段AE的长为 .
【答案】(1)∠AED=∠C(2)![]()
【解析】
(1)根据切线的性质和圆周角定理解答即可;
(2)根据勾股定理和三角函数进行解答即可.
(1)∠AED=∠C,证明如下:
连接BD,
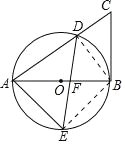
可得∠ADB=90°,
∴∠C+∠DBC=90°,
∵CB是⊙O的切线,
∴∠CBA=90°,
∴∠ABD+∠DBC=90°,
∴∠ABD=∠C,
∵∠AEB=∠ABD,
∴∠AED=∠C,
(2)连接BE,
∴∠AEB=90°,
∵∠C=60°,
∴∠CAB=30°,
在Rt△DAB中,AD=3,∠ADB=90°,
∴cos∠DAB=![]() ,
,
解得:AB=2![]() ,
,
∵E是半圆AB的中点,
∴AE=BE,
∵∠AEB=90°,
∴∠BAE=45°,
在Rt△AEB中,AB=2![]() ,∠ADB=90°,
,∠ADB=90°,
∴cos∠EAB=![]() ,
,
解得:AE=![]() .
.
故答案为:![]()


科目:初中数学 来源: 题型:
【题目】一条船上午![]() 点在
点在![]() 处望见西南方向有一座灯塔
处望见西南方向有一座灯塔![]() (如图),此时测得船和灯塔相距
(如图),此时测得船和灯塔相距![]() 海里,船以每小时
海里,船以每小时![]() 海里的速度向南偏西
海里的速度向南偏西![]() 的方向航行到
的方向航行到![]() 处,这时望见灯塔在船的正北方向.(参考数据:
处,这时望见灯塔在船的正北方向.(参考数据:![]() ,
,![]() ).
).

![]() 求几点钟船到达
求几点钟船到达![]() 处;
处;
![]() 求船到达
求船到达![]() 处时与灯塔
处时与灯塔![]() 之间的距离.
之间的距离.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在如图所示的直角坐标系中,解答下列问题.
(1)分别写出A、B两点的坐标:A ,B .
(2)△ABC的面积= ;点B到AC的距离= .
(3)画出△ABC关于x轴对称的△A1B1C1.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知![]() 和
和![]() 是两个边长都为
是两个边长都为![]() 的等边三角形,且点
的等边三角形,且点![]() ,
,![]() ,
,![]() ,
,![]() 在同一直线上,连接
在同一直线上,连接![]() ,
,![]() .
.
![]() 求证:四边形
求证:四边形![]() 是平行四边形;
是平行四边形;
![]() 若
若![]() 沿着
沿着![]() 的方向匀速运动,
的方向匀速运动,![]() 不动,当
不动,当![]() 运动到点
运动到点![]() 与点
与点![]() 重合时,四边形
重合时,四边形![]() 是什么特殊的四边形?说明理由.
是什么特殊的四边形?说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一辆慢车从甲地匀速行驶至乙地,一辆快车同时从乙地出发匀速行驶至甲地,两车之间的距离y(千米)与行驶时间x(小时)的对应关系如图所示,下列叙述正确的是( )

A. 甲乙两地相距1200千米
B. 快车的速度是80千米∕小时
C. 慢车的速度是60千米∕小时
D. 快车到达甲地时,慢车距离乙地100千米
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,在矩形ABCD中,动点P从点B出发,沿BC,CD,DA运动至点A停止.设点P运动的路程为x,△ABP的面积为y,如果y关于x的函数图象如图2所示.
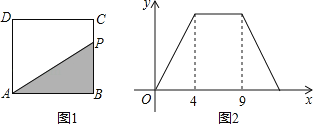
(1)求△ABC的面积;
(2)求y关于x的函数解析式;
(3)当△ABP的面积为5时,求x的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知半圆![]() 的直径
的直径![]() ,在
,在![]() 中,
中,![]() ,
,![]() ,
,![]() ,半圆
,半圆![]() 以
以![]() 的速度从左向右运动,在运动过程中,点
的速度从左向右运动,在运动过程中,点![]() 、
、![]() 始终在直线
始终在直线![]() 上.设运动时间为
上.设运动时间为![]() ,当
,当![]() 时,半圆
时,半圆![]() 在
在![]() 的左侧,
的左侧,![]() .
.
![]() 当
当![]() 为何值时,
为何值时,![]() 的一边所在直线与半圆
的一边所在直线与半圆![]() 所在的圆相切?
所在的圆相切?
![]() 当
当![]() 的一边所在直线与半圆
的一边所在直线与半圆![]() 所在的圆相切时,如果半圆
所在的圆相切时,如果半圆![]() 与直线
与直线![]() 围成的区域与
围成的区域与![]() 三边围成的区域有重叠部分,求重叠部分的面积.
三边围成的区域有重叠部分,求重叠部分的面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知AB∥CD,F为CD上一点,∠EFD=60°,∠AEC=2∠CEF,若6°<∠BAE<15°,∠C的度数为整数,则∠C的度数为_____.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某公司生产某种产品的成本是200元/件,售价是250元/件,年销售量为10万件.为了获得更好的效益,公司准备拿出一定的资金做广告.根据经验,每年投入的广告费用x万元,产品的年销售量将是原销售量的y倍,且y与x之间满足二次函数关系:y=﹣0.001x2+0.06x+1.
(1)如果把利润看作是销售总额减去成本费用和广告费用,试求出年利润S(万元)与广告费用x(万元)的函数关系式(无需自变量的取值范围);
(2)如果公司年投入的广告费不低于10万元且不高于50万元,求年利润S的最大值;
(3)若公司希望年利润在776万元到908万元之间(含端点),请从节约支出的角度直接写出广告费x的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com