
【题目】在![]() 中,
中,![]() 、
、![]() 、
、![]() 三边的长分别为
三边的长分别为![]() 、
、![]() 、
、![]() ,求这个三角形的面积.小辉同学在解答这道题时,先建立一个正方形网格(每个小正方形的边长为1),再在网格中画出格点
,求这个三角形的面积.小辉同学在解答这道题时,先建立一个正方形网格(每个小正方形的边长为1),再在网格中画出格点![]() (即
(即![]() 三个顶点都在小正方形的顶点处),如图①所示.这样不需求
三个顶点都在小正方形的顶点处),如图①所示.这样不需求![]() 的高,而借用网格就能计算出它的面积.
的高,而借用网格就能计算出它的面积.
(1)请你将![]() 的面积直接填写在横线上.__________________
的面积直接填写在横线上.__________________
(2)我们把上述求![]() 面积的方法叫做构图法.若
面积的方法叫做构图法.若![]() 三边的长分别为
三边的长分别为![]() 、
、![]() 、
、![]() (
(![]() ),请利用图②的正方形网格(每个小正方形的边长为
),请利用图②的正方形网格(每个小正方形的边长为![]() )画出相应的
)画出相应的![]() ,并求出它的面积.
,并求出它的面积.
(3) 若△ABC三边的长分别为![]() 、
、![]() 、
、![]() (m>0,n>0,且m≠n),请利用图③的长方形网格试运用构图法求出这三角形的面积.
(m>0,n>0,且m≠n),请利用图③的长方形网格试运用构图法求出这三角形的面积.

【答案】(1)![]() ;(2)图见解析;3a2;(3)图见解析;3mn.
;(2)图见解析;3a2;(3)图见解析;3mn.
【解析】
(1)依据△ABC的面积=3×31×2÷21×3÷22×3÷2进行计算即可;
(2)![]() 是直角边长为a,2a的直角三角形的斜边;
是直角边长为a,2a的直角三角形的斜边;![]() 是直角边长为2a,2a的直角三角形的斜边;
是直角边长为2a,2a的直角三角形的斜边;![]() 是直角边长为a,4a的直角三角形的斜边,把它整理为一个矩形的面积减去三个直角三角形的面积;
是直角边长为a,4a的直角三角形的斜边,把它整理为一个矩形的面积减去三个直角三角形的面积;
(3)![]() 是以m,2n为直角边的直角三角形的斜边长;
是以m,2n为直角边的直角三角形的斜边长; ![]() 是以m,4n为直角边的直角三角形的斜边长;
是以m,4n为直角边的直角三角形的斜边长;![]() 是以2m,2n为直角边的直角三角形的斜边长;继而可作出三角形,然后求得三角形的面积.
是以2m,2n为直角边的直角三角形的斜边长;继而可作出三角形,然后求得三角形的面积.
(1)△ABC的面积=3×31×2÷21×3÷22×3÷2=![]() ,
,
故答案为:![]() ;
;
(2)如图:
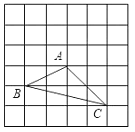
由图可得,S△=2a×4a![]()
![]()
![]() =3a2;
=3a2;
(3)如图,
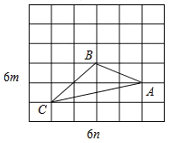
AB=![]() ,AC=
,AC=![]() ,BC=2
,BC=2![]() ,
,
∴S△ABC=2m×4n![]() ×2m×2n
×2m×2n![]() ×m×4n
×m×4n![]() ×m×2n=3mn.
×m×2n=3mn.


科目:初中数学 来源: 题型:
【题目】如图1,在矩形ABCD中,动点P从点B出发,沿BC,CD,DA运动至点A停止.设点P运动的路程为x,△ABP的面积为y,如果y关于x的函数图象如图2所示.
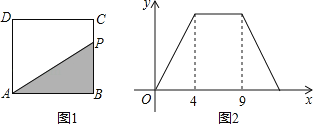
(1)求△ABC的面积;
(2)求y关于x的函数解析式;
(3)当△ABP的面积为5时,求x的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
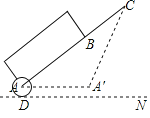
【题目】拉杆箱是人们出行的常用品,采用拉杆箱可以让人们出行更轻松.如图,一直某种拉杆箱箱体长AB=65cm,拉杆最大伸长距离BC=35cm,在箱体底端装有一圆形滚轮,当拉杆拉到最长时,滚轮的圆心在图中的A处,点A到地面的距离AD=3cm,当拉杆全部缩进箱体时,滚轮圆心水平向右平移55cm到A′处,求拉杆把手C离地面的距离(假设C点的位置保持不变).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,如图所示的函数图象是由函数y=(x﹣1)2+1(x≥0)的图象C1和图象C2组成中心对称图形,对称中心为点(0,2).已知不重合的两点A、B分别在图象C1和C2上,点A、B的横坐标分别为a、b,且a+b=0.当b<x≤a时该函数的最大值和最小值均与a、b的值无关,则a的取值范围为_____.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某公司生产某种产品的成本是200元/件,售价是250元/件,年销售量为10万件.为了获得更好的效益,公司准备拿出一定的资金做广告.根据经验,每年投入的广告费用x万元,产品的年销售量将是原销售量的y倍,且y与x之间满足二次函数关系:y=﹣0.001x2+0.06x+1.
(1)如果把利润看作是销售总额减去成本费用和广告费用,试求出年利润S(万元)与广告费用x(万元)的函数关系式(无需自变量的取值范围);
(2)如果公司年投入的广告费不低于10万元且不高于50万元,求年利润S的最大值;
(3)若公司希望年利润在776万元到908万元之间(含端点),请从节约支出的角度直接写出广告费x的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校把一块形状为直角三角形的废地开辟为生物园,如图所示,∠ACB=90°,AC=40m,BC=30m.线段CD是一条水渠,且D点在边AB上,已知水渠的造价为800元![]() ,问:当水渠的造价最低时,CD长为多少米?最低造价是多少元?
,问:当水渠的造价最低时,CD长为多少米?最低造价是多少元?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】将正方形ABCD放在如图所示的直角坐标系中,A点的坐标为(4,0),N点的坐标为(3,0),MN平行于y轴,E是BC的中点,现将纸片折叠,使点C落在MN上,折痕为直线EF.
(1)求点G的坐标;
(2)求直线EF的解析式;
(3)设点P为直线EF上一点,是否存在这样的点P,使以P, F, G的三角形是等腰三角形?若存在,直接写出P点的坐标;若不存在,请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为迎接G20杭州峰会的召开,某校八年级(1)(2)班准备集体购买一种T恤衫参加一项社会活动.了解到某商店正好有这种T恤衫的促销,当购买10件时每件140元,购买数量每增加1件单价减少1元;当购买数量为60件(含60件)以上时,一律每件80元.
(1)如果购买x件(10<x<60),每件的单价为y元,请写出y关于x的函数关系式;
(2)如果八(1)(2)班共购买了100件T恤衫,由于某种原因需分两批购买,且第一批购买数量多于30件且少于60件.已知购买两批T恤衫一共花了9200元,求第一批T恤衫的购买数量.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com