
【题目】将正方形ABCD放在如图所示的直角坐标系中,A点的坐标为(4,0),N点的坐标为(3,0),MN平行于y轴,E是BC的中点,现将纸片折叠,使点C落在MN上,折痕为直线EF.
(1)求点G的坐标;
(2)求直线EF的解析式;
(3)设点P为直线EF上一点,是否存在这样的点P,使以P, F, G的三角形是等腰三角形?若存在,直接写出P点的坐标;若不存在,请说明理由.

【答案】(1)G点的坐标为:(3,4-![]() );(2)EF的解析式为:y=
);(2)EF的解析式为:y=![]() x+4-2
x+4-2![]() ;(3)P1(1,4-
;(3)P1(1,4-![]() )、P2(
)、P2(![]() ,7-2
,7-2![]() ),P3(-
),P3(-![]() ,2
,2![]() -1)、P4(3,4+
-1)、P4(3,4+![]() )
)
【解析】分析:(1)点G的横坐标与点N的横坐标相同,易得EM为BC的一半减去1,为1,EG=CE=2,利用勾股定理可得MG的长度,4减MG的长度即为点G的纵坐标;
(2)由△EMG的各边长可得∠MEG的度数为60°,进而可求得∠CEF的度数,利用相应的三角函数可求得CF长,4减去CF长即为点F的纵坐标,设出直线解析式,把E,F坐标代入即可求得相应的解析式;
(3)以点F为圆心,FG为半径画弧,交直线EF于两点;以点G为圆心,FG为半径画弧,交直线EF于一点;做FG的垂直平分线交直线EF于一点,根据线段的长度和与坐标轴的夹角可得相应坐标.
详解:(1)易得EM=1,CE=2,
∵EG=CE=2,
∴MG=![]() ,
,
∴GN=4-![]() ;
;
G点的坐标为:(3,4-![]() );
);
(2)易得∠MEG的度数为60°,
∵∠CEF=∠FEG,
∴∠CEF=60°,
∴CF=2![]() ,
,
∴OF=4-2![]() ,
,
∴点F(0,4-2![]() ).
).
设EF的解析式为y=kx+4-2![]() ,
,
易得点E的坐标为(2,4),
把点E的坐标代入可得k=![]() ,
,
∴EF的解析式为:y=![]() x+4-2
x+4-2![]() .
.
(3)P1(1,4-![]() )、P2(
)、P2(![]() ,7-2
,7-2![]() ),
),
P3(-![]() ,2
,2![]() -1)、P4(3,4+
-1)、P4(3,4+![]() )
)


科目:初中数学 来源: 题型:
【题目】王红有5张写着以下数字的卡片,请按要求抽出卡片,完成下列各题:![]()
(1)从中取出2张卡片,使这2张卡片上数字乘积最小,最小值是 .
(2)从中取出2张卡片,使这2张卡片数字相除商最大,最大值是 .
(3)从中取出除0以外的4张卡片,将这4个数字进行加、减、乘、除或乘方等混合运算,使结果为24,(注:每个数字只能用一次,如:23×[1﹣(﹣2)]),请另写出一种符合要求的运算式子 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】将直角边长为6的等腰直角△AOC放在平面直角坐标系中,点O为坐标原点,点C、A分别在x轴,y轴的正半轴上,一条抛物线经过点A、C及点B(﹣3,0).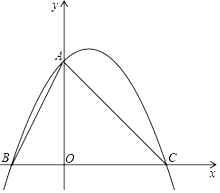
(1)求该抛物线的解析式;
(2)若点P是线段BC上一动点,过点P作AB的平行线交AC于点E,连接AP,当△APE的面积最大时,求点P的坐标;
(3)若点P(t,t)在抛物线上,则称点P为抛物线的不动点,将(1)中的抛物线进行平移,平移后,该抛物线只有一个不动点,且顶点在直线y=2x﹣ ![]() 上,求此时抛物线的解析式.
上,求此时抛物线的解析式.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】把下列各数分别填入相应的集合里:+(-2),0,﹣0.314,![]() (两个1间的0的个数依次多1个)﹣(﹣11),
(两个1间的0的个数依次多1个)﹣(﹣11),![]() ,
,![]() ,
,![]() ,
,![]()
正有理数集合:{ …},
无理数集合: { …},
整数集合: { …},
分数集合: { …}.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在5×4的网格中,每个小正方形的边长是1个单位长.
(1)先在图中将面积是5的一个长方形分割成5块,然后再画出用这5块拼成的一个正方形;

(2)设拼成的正方形的边长为a个单位长,
①a是有理数还是无理数?
②试在数轴上将a的相反数表示出来;
③求出a的近似值(保留一位小数)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB=AC,AE是∠BAC的平分线,∠ABC的平分线BM交AE于点M,点O在AB上,以点O为圆心,OB的长为半径的圆经过点M,交BC于点G,交AB于点F. 
(1)求证:AE为⊙O的切线;
(2)当BC=4,AC=6时,求⊙O的半径;
(3)在(2)的条件下,求线段BG的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知函数y= ![]() 的图形如图,以下结论: ①m<0;
的图形如图,以下结论: ①m<0;
②在每个分支上y随x的增大而增大;
③若点A(﹣1,a),点B(2,b)在图象上,则a<b;
④若点P(x,y)在图象上,则点P1(﹣x,﹣y)也在图象上.其中正确的个数是( )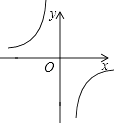
A.1个
B.2个
C.3个
D.4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如下图是用棋子摆成的“T”字图案.从图案中可以看出,第一个“T”字图案需要5枚棋子,第二个“T”字图案需要8枚棋子,第三个“T”字图案需要11枚棋子

(1)照此规律,摆成第八个图案需要几枚棋子?
(2)摆成第n个图案需要几枚棋子?
(3)摆成第2008个图案需要几枚棋子?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图在数轴上A点表示数![]() ,B点表示数
,B点表示数![]() ,
,![]() 、
、![]() 满足|
满足|![]() |+|
|+|![]() |=0;
|=0;
![]()
(1)点A表示的数为_____;点B表示的数为_____;
(2)若在原点O处放一挡板,一小球甲从点A处以1个单位/秒的速度向左运动;同时另一小球乙从点B处以2个单位/秒的速度也向左运动,在碰到挡板后(忽略球的大小,可看作一点)以原来的速度向相反的方向运动,设运动的时间为t(秒),
①当t=1时,甲小球到原点的距离=_____;乙小球到原点的距离=_____.
当t=3时,甲小球到原点的距离=_____;乙小球到原点的距离=_____.
②试探究:甲,乙两小球到原点的距离可能相等吗?若不能,请说明理由.若能,请直接写出甲,乙两小球到原点的距离相等时经历的时间.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com