
【题目】将直角边长为6的等腰直角△AOC放在平面直角坐标系中,点O为坐标原点,点C、A分别在x轴,y轴的正半轴上,一条抛物线经过点A、C及点B(﹣3,0).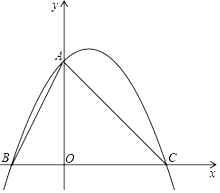
(1)求该抛物线的解析式;
(2)若点P是线段BC上一动点,过点P作AB的平行线交AC于点E,连接AP,当△APE的面积最大时,求点P的坐标;
(3)若点P(t,t)在抛物线上,则称点P为抛物线的不动点,将(1)中的抛物线进行平移,平移后,该抛物线只有一个不动点,且顶点在直线y=2x﹣ ![]() 上,求此时抛物线的解析式.
上,求此时抛物线的解析式.
【答案】
(1)
解:∵B(﹣3,0),C(6,0),设抛物线为y=a(x+3)(x﹣6),过A(0,6)
∴6=a(0+3)(0﹣6),
解得a=﹣ ![]() ,
,
∴y=﹣ ![]() (x+3)(x﹣6),
(x+3)(x﹣6),
即y=﹣ ![]() x2+x+6;
x2+x+6;
(2)
解:设P(m,0),
如图,

∵PE∥AB,
∴△PCE∽△BCA,
∴ ![]() ,
,
![]() ,
,
∴S△PCE= ![]() ,
,
∴S=S△APC﹣S△PCE=﹣ ![]() m2+m+6,
m2+m+6,
=﹣ ![]() (m﹣
(m﹣ ![]() )2+
)2+ ![]() ,
,
∴当m= ![]() 时,S有最大值为
时,S有最大值为 ![]() ;
;
∴P( ![]() ,0)
,0)
(3)
解:设平移后的抛物线的顶点为G(h,k),
∴抛物线解析式为y=﹣ ![]() (x﹣h)2+k,
(x﹣h)2+k,
由抛物线的不动点的定义,得,t=﹣ ![]() (t﹣h)2+k,
(t﹣h)2+k,
即:t2+(3﹣2h)t+h2﹣3k=0,
∵平移后,抛物线只有一个不动点,
∴此方程有两个相等的实数根,
∴△=(3﹣2h)2﹣4(h2﹣3k)=0,
∴h﹣k= ![]() ①,
①,
∵顶点在直线y=2x﹣ ![]() 上,
上,
∴k=2k﹣ ![]() ②,
②,
∴联立①②得,h=1,k= ![]() ,
,
∴抛物线的解析式为y=﹣ ![]() (x﹣1)2+
(x﹣1)2+ ![]() =﹣
=﹣ ![]() x2+
x2+ ![]() x﹣
x﹣ ![]()
【解析】(1)已知抛物线与x轴的两个交点坐标,所以设抛物线方程为两点式:y=a(x+3)(x﹣6),然后把点A的坐标代入该函数解析式即可求得系数a的值;(2)利用相似三角形的性质得出S△PCE= ![]() ,进而求出△APE的面积S,即可得出点P坐标;(3)利用抛物线上不动点的定义以及不动点的个数得出方程h﹣k=
,进而求出△APE的面积S,即可得出点P坐标;(3)利用抛物线上不动点的定义以及不动点的个数得出方程h﹣k= ![]() ①,再用平移后的抛物线的顶点在直线y=2x﹣
①,再用平移后的抛物线的顶点在直线y=2x﹣ ![]() 上,得出方程k=2k﹣
上,得出方程k=2k﹣ ![]() ②,联立解方程组即可.
②,联立解方程组即可.
【考点精析】本题主要考查了抛物线与坐标轴的交点和相似三角形的判定的相关知识点,需要掌握一元二次方程的解是其对应的二次函数的图像与x轴的交点坐标.因此一元二次方程中的b2-4ac,在二次函数中表示图像与x轴是否有交点.当b2-4ac>0时,图像与x轴有两个交点;当b2-4ac=0时,图像与x轴有一个交点;当b2-4ac<0时,图像与x轴没有交点.;相似三角形的判定方法:两角对应相等,两三角形相似(ASA);直角三角形被斜边上的高分成的两个直角三角形和原三角形相似; 两边对应成比例且夹角相等,两三角形相似(SAS);三边对应成比例,两三角形相似(SSS)才能正确解答此题.


科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,借助直角三角板可以找到一元二次方程的实数根,比如对于方程 ![]() ,操作步骤是:
,操作步骤是:
第一步:根据方程系数特征,确定一对固定点A(0,1),B(5,2);
第二步:在坐标平面中移动一个直角三角板,使一条直角边恒过点A,另一条直角边恒过点B;
第三步:在移动过程中,当三角板的直角顶点落在x轴上点C处时,点C 的横坐标m即为该方程的一个实数根(如图1)
第四步:调整三角板直角顶点的位置,当它落在x轴上另一点D处时,点D 的横坐标为n即为该方程的另一个实数根。
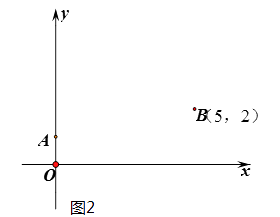
(1)在图2 中,按照“第四步“的操作方法作出点D(请保留作出点D时直角三角板两条直角边的痕迹)
(2)结合图1,请证明“第三步”操作得到的m就是方程 ![]() 的一个实数根;
的一个实数根;
(3)上述操作的关键是确定两个固定点的位置,若要以此方法找到一元二次方程 ![]() 的实数根,请你直接写出一对固定点的坐标;
的实数根,请你直接写出一对固定点的坐标;
(4)实际上,(3)中的固定点有无数对,一般地,当 ![]() ,
, ![]() ,
, ![]() ,
, ![]() 与a,b,c之间满足怎样的关系时,点P(
与a,b,c之间满足怎样的关系时,点P( ![]() ,
, ![]() ),Q(
),Q( ![]() ,
, ![]() )就是符合要求的一对固定点?
)就是符合要求的一对固定点?
查看答案和解析>>
科目:初中数学 来源: 题型:
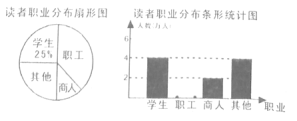
【题目】学习成为现代人的时尚,我,市有关部门统计了最近6个月到图书馆的读者和职业分布情况,并做了下列两个不完整的统计图.请你根据图中提供的信息,解答下列问题:
(l)求在统汁的这段时问内,到图书馆阅读的总人次:
(2)请补全条形统汁图,并求扇形统计图中表示“商人”的扇形的圆心角度数;
(3)符5月份到图书馆的读者共20000人次,估汁其中约有多少人次读者是职工?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知△ABC,△EFG均是边长为4的等边三角形,点D是边BC、EF的中点. (Ⅰ)如图①,这两个等边三角形的高为;
(Ⅱ)如图②,直线AG,FC相交于点M,当△EFG绕点D旋转时,线段BM长的最小值是 . 
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,要建一个长方形养鸡场,养鸡场的一边靠墙(墙长25米),另三边用竹篱笆围成,竹篱笆的长为40米,若要围成的养鸡场的面积为180平方米,求养鸡场的宽各为多少米,设与墙平行的一边长为x米. 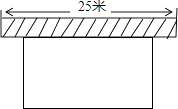
(1)填空:(用含x的代数式表示)另一边长为米;
(2)列出方程,并求出问题的解.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在菱形ABCD中,AB=4cm,∠ADC=120°,点E、F同时由A、C两点出发,分别沿AB、CB方向向点B匀速移动(到点B为止),点E的速度为1cm/s,点F的速度为2cm/s,经过t秒△DEF为等边三角形,则t的值为 .

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】二次函数y=ax2+bx+c(a≠0)的部分图象如图所示,图象过点(﹣1,0),对称轴为直线x=2,系列结论:(1)4a+b=0;(2)4a+c>2b;(3)5a+3c>0;(4)若点A(﹣2,y1),点B( ![]() ,y2),点C(
,y2),点C( ![]() ,y2)在该函数图象上,则y1<y3<y2;(5)若m≠2,则m(am+b)>2(2a+b),其中正确的结论有( )
,y2)在该函数图象上,则y1<y3<y2;(5)若m≠2,则m(am+b)>2(2a+b),其中正确的结论有( ) 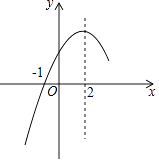
A.2个
B.3个
C.4个
D.5个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】将正方形ABCD放在如图所示的直角坐标系中,A点的坐标为(4,0),N点的坐标为(3,0),MN平行于y轴,E是BC的中点,现将纸片折叠,使点C落在MN上,折痕为直线EF.
(1)求点G的坐标;
(2)求直线EF的解析式;
(3)设点P为直线EF上一点,是否存在这样的点P,使以P, F, G的三角形是等腰三角形?若存在,直接写出P点的坐标;若不存在,请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为积极响应政府提出的“绿色发展·低碳出行”号召,某社区决定购置一批共享单车,经市场调查得知,购买3量男式单车与4辆女式单车费用相同,购买5辆男式单车与4辆女式单车共需16000元.
(1)求男式单车和女式单车的单价;
(2)该社区要求男式单比女式单车多4辆,两种单车至少需要22辆,购置两种单车的费用不超过50000元,该社区有几种购置方案?怎样购置才能使所需总费用最低,最低费用是多少?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com