
【题目】如下图是用棋子摆成的“T”字图案.从图案中可以看出,第一个“T”字图案需要5枚棋子,第二个“T”字图案需要8枚棋子,第三个“T”字图案需要11枚棋子

(1)照此规律,摆成第八个图案需要几枚棋子?
(2)摆成第n个图案需要几枚棋子?
(3)摆成第2008个图案需要几枚棋子?
【答案】(1)摆成第八个图案需要26枚棋子;(2)(3n+2)枚棋子;(3)第2008个图案需6026枚棋子.
【解析】
由图形可知:第1个“T”字型图案需要3+2=5枚棋子,第2个“T”字型图案需要3×2+2=8枚棋子,第3个“T”字型图案需要3×3+2=11枚棋子,…由此得出第n个“Τ”字型所需棋子的个数为3n+2枚.
解:(1)首先观察图形,得到前面三个图形的具体个数,不难发现:在5的基础上依次多3枚.即第n个图案需要5+3(n﹣1)=3n+2.那么当n=8时,则有26枚;当n=2008时,需要6026枚.故摆成第八个图案需要26枚棋子
(2)因为第①个图案有5枚棋子,第②个图案有(5+3×1)枚棋子,第③个图案有(5+3×2)枚棋子,依此规律可得第n个图案需5+3×(n﹣1)=5+3n﹣3=(3n+2)枚棋子
(3)3×2008+2=6026(枚)即第2008个图案需6026枚棋子.


 中考解读考点精练系列答案
中考解读考点精练系列答案科目:初中数学 来源: 题型:
【题目】已知△ABC,△EFG均是边长为4的等边三角形,点D是边BC、EF的中点. (Ⅰ)如图①,这两个等边三角形的高为;
(Ⅱ)如图②,直线AG,FC相交于点M,当△EFG绕点D旋转时,线段BM长的最小值是 . 
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】将正方形ABCD放在如图所示的直角坐标系中,A点的坐标为(4,0),N点的坐标为(3,0),MN平行于y轴,E是BC的中点,现将纸片折叠,使点C落在MN上,折痕为直线EF.
(1)求点G的坐标;
(2)求直线EF的解析式;
(3)设点P为直线EF上一点,是否存在这样的点P,使以P, F, G的三角形是等腰三角形?若存在,直接写出P点的坐标;若不存在,请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在数轴上,点![]() 表示
表示![]() ,现将点
,现将点![]() 沿
沿![]() 轴做如下移动,第一次点
轴做如下移动,第一次点![]() 向左移动
向左移动![]() 个单位长度到达点
个单位长度到达点![]() ,第二次将点
,第二次将点![]() ,向右移动
,向右移动![]() 个单位长度到达点
个单位长度到达点![]() ,第三次将点
,第三次将点![]() 向左移动
向左移动![]() 个单位长度到达点
个单位长度到达点![]() ,按照这种移动规律移动下去,第
,按照这种移动规律移动下去,第![]() 次移动到点
次移动到点![]() ,如果点
,如果点![]() 与原点的距离等于
与原点的距离等于![]() ,那么
,那么![]() 的值是________.
的值是________.
![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图①为一种平板电脑保护套的支架效果图,AM固定于平板电脑背面,与可活动的MB、CB部分组成支架.平板电脑的下端N保持在保护套CB上,不考虑拐角处的弧度及平板电脑和保护套的厚度,绘制成图②,其中AN表示平板电脑,M为AN上的定点,AN=CB=20cm,AM=8cm,MB=MN,我们把∠ANB叫做倾斜角,根据以上数据,判断倾斜角能小于30°吗?请说明理由.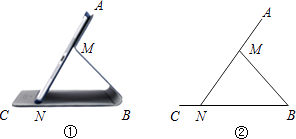
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】数学实验室:
点A、B在数轴上分别表示有理数a、b,A、B两点之间的距离表示为AB,在数轴上A、B两点之间的距离AB=|a﹣b|.
利用数形结合思想回答下列问题:
(1)数轴上表示2和5的两点之间的距离是_________,数轴上表示1和-3的两点之间的距离是 ;
(2)数轴上若点A表示的数是x,点B表示的数是-2,则点A和B之间的距离是 ,若AB=2,那么x为 ;
(3)当x是 时,代数式![]() ;
;
(4)若点A表示的数-1,点B与点A的距离是10,且点B在点A的右侧,动点P、Q同时从A、B出发沿数轴正方向运动,点P的速度是每秒3个单位长度,点Q的速度是每秒1个单位长度,求运动几秒后,PQ=1?(请写出必要的求解过程)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为积极响应政府提出的“绿色发展·低碳出行”号召,某社区决定购置一批共享单车,经市场调查得知,购买3量男式单车与4辆女式单车费用相同,购买5辆男式单车与4辆女式单车共需16000元.
(1)求男式单车和女式单车的单价;
(2)该社区要求男式单比女式单车多4辆,两种单车至少需要22辆,购置两种单车的费用不超过50000元,该社区有几种购置方案?怎样购置才能使所需总费用最低,最低费用是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】把下列各数填在相应的大括号中:
8, ![]() , +2.8, π,
, +2.8, π, ![]() , -0.003, 0,-100, -(-6), -3.626626662…
, -0.003, 0,-100, -(-6), -3.626626662…
正数集合{___________________________________________________…}
整数集合{___________________________________________________…}
负分数集合{_________________________________________________…}
无理数集合{_________________________________________________…}.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知顶点为(﹣3,﹣6)的抛物线y=ax2+bx+c经过点(﹣1,﹣4),则下列结论中错误的是( ) 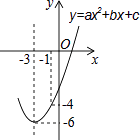
A.b2>4ac
B.ax2+bx+c≥﹣6
C.关于x的一元二次方程ax2+bx+c=﹣4的两根分别为﹣5和﹣1
D.若点(﹣2,m),(﹣5,n)在抛物线上,则m>n
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com