
【题目】王红有5张写着以下数字的卡片,请按要求抽出卡片,完成下列各题:![]()
(1)从中取出2张卡片,使这2张卡片上数字乘积最小,最小值是 .
(2)从中取出2张卡片,使这2张卡片数字相除商最大,最大值是 .
(3)从中取出除0以外的4张卡片,将这4个数字进行加、减、乘、除或乘方等混合运算,使结果为24,(注:每个数字只能用一次,如:23×[1﹣(﹣2)]),请另写出一种符合要求的运算式子 .
【答案】(1)﹣6;(2)3;(3) [3﹣(﹣2)]2﹣1=24(答案不唯一,符合题意正确即可).
【解析】
(1)观察这五个数,要找乘积最小的就要找符号相反且数值最大的数,所以选3和-2,再计算即可;(2)观察这五个数,2张卡片上数字相除的商最大就要找符号相同,且分子越大越好,分母越小越好,所以就要选3和1,且1为分母;(3)从中取出4张卡片,用学过的运算方法,使结果为24,这就不唯一,用加减乘除只要答数是24即可,比如3、-2、2、1,四个数,[3﹣(﹣2)]2﹣1=24.
(1)取3,﹣2,乘积最小=﹣6,
故答案为﹣6.
(2)取3,1商的最大值为3,
故答案为3.
(3)[3﹣(﹣2)]2﹣1=24.


科目:初中数学 来源: 题型:
【题目】阅读下列材料,解答下面的问题:
我们知道方程![]() 有无数个解,但在实际生活中我们往往只需求出其
有无数个解,但在实际生活中我们往往只需求出其
正整数解.
例:由![]() ,得:
,得:![]() ,(x、y为正整数)
,(x、y为正整数)
∴![]() ,则有
,则有![]() .又
.又![]() 为正整数,则
为正整数,则![]() 为正整数.由2与3互质,可知:x为3的倍数,从而x=3,代入
为正整数.由2与3互质,可知:x为3的倍数,从而x=3,代入![]() ∴2x+3y=12的正整数解为
∴2x+3y=12的正整数解为![]()
问题:
(1)请你写出方程![]() 的一组正整数解: .
的一组正整数解: .
(2)若![]() 为自然数,则满足条件的x值为 .
为自然数,则满足条件的x值为 .
(3)七年级某班为了奖励学习进步的学生,购买了单价为3元的笔记本与单价为5元的钢笔两种奖品,共花费35元,问有几种购买方案?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,借助直角三角板可以找到一元二次方程的实数根,比如对于方程 ![]() ,操作步骤是:
,操作步骤是:
第一步:根据方程系数特征,确定一对固定点A(0,1),B(5,2);
第二步:在坐标平面中移动一个直角三角板,使一条直角边恒过点A,另一条直角边恒过点B;
第三步:在移动过程中,当三角板的直角顶点落在x轴上点C处时,点C 的横坐标m即为该方程的一个实数根(如图1)
第四步:调整三角板直角顶点的位置,当它落在x轴上另一点D处时,点D 的横坐标为n即为该方程的另一个实数根。
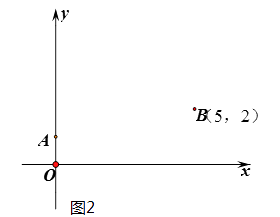
(1)在图2 中,按照“第四步“的操作方法作出点D(请保留作出点D时直角三角板两条直角边的痕迹)
(2)结合图1,请证明“第三步”操作得到的m就是方程 ![]() 的一个实数根;
的一个实数根;
(3)上述操作的关键是确定两个固定点的位置,若要以此方法找到一元二次方程 ![]() 的实数根,请你直接写出一对固定点的坐标;
的实数根,请你直接写出一对固定点的坐标;
(4)实际上,(3)中的固定点有无数对,一般地,当 ![]() ,
, ![]() ,
, ![]() ,
, ![]() 与a,b,c之间满足怎样的关系时,点P(
与a,b,c之间满足怎样的关系时,点P( ![]() ,
, ![]() ),Q(
),Q( ![]() ,
, ![]() )就是符合要求的一对固定点?
)就是符合要求的一对固定点?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,矩形ABCD中,AB=4,BC=3,点E,F,G,H分别在矩形ABCD各边上,且AE=CG,BF=DH,则四边形EFGH周长的最小值为( )
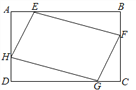
A. 7 B. 10 C. 14 D. 15
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,以AB为直径的⊙O经过AC的中点D,DE⊥BC于点E. 
(1)求证:DE是⊙O的切线;
(2)当AB=4 ![]() ,∠C=30°时,求图中阴影部分的面积(结果保留根号和π).
,∠C=30°时,求图中阴影部分的面积(结果保留根号和π).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某市甲、乙两个汽车销售公司,去年一至十月份每月销售同种品牌汽车的情况如图所示:
![]() 请你根据上图填写下表:
请你根据上图填写下表:
销售公司 | 平均数 | 方差 | 中位数 | 众数 |
甲 |
| 9 | ||
乙 | 9 |
| 8 |
![]() 请你从以下两个不同的方面对甲、乙两个汽车销售公司去年一至十月份的销售情况进行分析:
请你从以下两个不同的方面对甲、乙两个汽车销售公司去年一至十月份的销售情况进行分析:
![]() 从平均数和方差结合看;
从平均数和方差结合看;
![]() 从折线图上甲、乙两个汽车销售公司销售数量的趋势看
从折线图上甲、乙两个汽车销售公司销售数量的趋势看![]() 分析哪个汽车销售公司较有潜力
分析哪个汽车销售公司较有潜力![]() .
.

查看答案和解析>>
科目:初中数学 来源: 题型:
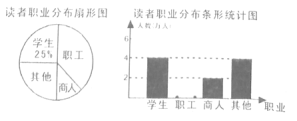
【题目】学习成为现代人的时尚,我,市有关部门统计了最近6个月到图书馆的读者和职业分布情况,并做了下列两个不完整的统计图.请你根据图中提供的信息,解答下列问题:
(l)求在统汁的这段时问内,到图书馆阅读的总人次:
(2)请补全条形统汁图,并求扇形统计图中表示“商人”的扇形的圆心角度数;
(3)符5月份到图书馆的读者共20000人次,估汁其中约有多少人次读者是职工?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知△ABC,△EFG均是边长为4的等边三角形,点D是边BC、EF的中点. (Ⅰ)如图①,这两个等边三角形的高为;
(Ⅱ)如图②,直线AG,FC相交于点M,当△EFG绕点D旋转时,线段BM长的最小值是 . 
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】将正方形ABCD放在如图所示的直角坐标系中,A点的坐标为(4,0),N点的坐标为(3,0),MN平行于y轴,E是BC的中点,现将纸片折叠,使点C落在MN上,折痕为直线EF.
(1)求点G的坐标;
(2)求直线EF的解析式;
(3)设点P为直线EF上一点,是否存在这样的点P,使以P, F, G的三角形是等腰三角形?若存在,直接写出P点的坐标;若不存在,请说明理由.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com