
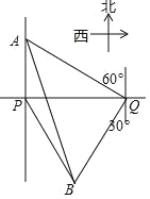
【题目】一轮船在P处测得灯塔A在正北方向,灯塔B在南偏东30°方向,轮船向正东航行了900m,到达Q处,测得A位于北偏西60°方向, B位于南偏西30°方向.
(1)线段BQ与PQ是否相等?请说明理由;
(2)求A、B间的距离(结果保留根号).
科目:初中数学 来源: 题型:
【题目】如图①所示是一个长为2m,宽为2n的长方形,沿图中虚线用剪刀均分成四个小长方形,然后按图②的方式拼成一个正方形.

(1)你认为图②中的阴影部分的正方形的边长等于_________________;
(2)请用两种不同的方法列代数式表示图②中阴影部分的面积.
方法① __________________.方法② _____________________;
(3)观察图②,你能写出(m+n)2,(m-n)2,mn这三个代数式之间的等量关系吗?
答:________________________ .
(4)根据(3)题中的等量关系,解决如下问题:若a+b=6,ab=4,则求(a-b)2的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)计算(﹣![]() )﹣2﹣16÷(﹣2)3+(π﹣tan60°)0﹣2
)﹣2﹣16÷(﹣2)3+(π﹣tan60°)0﹣2![]() cos30°;
cos30°;
(2)先化简,再求值:![]() ÷
÷![]() ﹣
﹣![]() ,其中x满足方程x2+4x﹣5=0.
,其中x满足方程x2+4x﹣5=0.
查看答案和解析>>
科目:初中数学 来源: 题型:
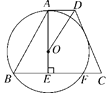
【题目】如图,梯形ABCD中,AD∥BC,AE⊥BC于点E,∠ADC的平分线交AE于点O,以点O为圆心,OA为半径的圆经过点B,交BC于另一点F.
(1)求证:CD与⊙O相切;
(2)若BF=24,OE=5,求tan∠ABC的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】周末,我和爸爸、妈妈争夺唯一的一台电脑使用权,决定用游戏确定谁来使用电脑.
(1)若使用三张完全相同纸条,其中一张标注为“是”,另外两张空白,则爸爸抓到标注为“是”的概率是 .
(2)任意投掷两枚质地均匀的硬币,若两枚正面都朝上,则爸爸使用电脑;若两枚反面都朝上,妈妈使用电脑;若一枚正面朝上一枚反面朝上,则我使用电脑.请你请用列表或画树状图的方法计算妈妈使用电脑的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】把2只大杯和6只小杯装满水,正好是2000毫升,每只大杯比小杯多装200毫升,现在有![]() 只大杯和
只大杯和![]() 只小杯,装满水,正好是8000毫升,下面有四组关于
只小杯,装满水,正好是8000毫升,下面有四组关于![]() 、
、![]() 的取值,其中不正确的是
的取值,其中不正确的是
A.![]() B.
B.![]()
C.![]() D.
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,直线![]() 的图像与反比例函数
的图像与反比例函数![]() 的图像分别交于点A(2,m)、B(-4,-1),其中
的图像分别交于点A(2,m)、B(-4,-1),其中![]()
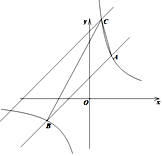
(1)求m的值和直线的解析式;
(2)若![]() ,观察图像,请直接写出x的取值范围;
,观察图像,请直接写出x的取值范围;
(3)将直线![]() 的图像向上平移与反比例函数的图像在第一象限内交于点C,C点的横坐标为1,
的图像向上平移与反比例函数的图像在第一象限内交于点C,C点的横坐标为1,
①判定△ABC的形状并说明理由,②求△ABC的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
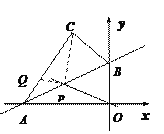
【题目】如图,已知直线![]() 与x轴、y轴分别交于A, B两点,将△AOB沿直线AB翻折,使点O落在点C处, 点P,Q分别在AB , AC上,当PC+PQ取最小值时,直线OP的解析式为( )
与x轴、y轴分别交于A, B两点,将△AOB沿直线AB翻折,使点O落在点C处, 点P,Q分别在AB , AC上,当PC+PQ取最小值时,直线OP的解析式为( )
A. y=- ![]() B. y=-
B. y=- ![]() C. y=-
C. y=- ![]() D.
D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB=AC,AB的垂直平分线MN交AC于点D,交AB于点E.
(1)若∠A=40°,求∠DBC的度数;
(2)若AE=6,△CBD的周长为20,求BC的长.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com