练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    【题目】（1）计算（﹣）﹣2﹣16÷（﹣2）3+（π﹣tan60°）0﹣2cos30°；

    （2）先化简，再求值：÷﹣，其中x满足方程x2+4x﹣5=0．

    【答案】（1）9；（2）原式=

    【解析】试题分析：（1）第一项负整数指数幂等于这个数的正整数指数幂的倒数；第二项先算乘方，再算除法；第三项非零数的零次幂等于1；第四项根据特殊角的三角函数值计算；（2）把除法转化为乘法，并把分子、分母分解因式约分，再算减法，然后求出一元二次方程的根，取一个使分式有意义的值代入计算.

    解：（1）原式=9+2+1﹣3=9；

    （2）原式=﹣=﹣=，

    方程x2+4x﹣5=0，变形得：（x﹣1）（x+5）=0，

    解得：x=1或x=﹣5，

    经检验x=1不合题意，舍去，

    则当x=﹣5时，原式=﹣．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    【题目】为充分发挥市场机制和价格杠杆在水资源配置中的作用，促进节约用水，提高用水效率，2017年7月1日起某地实行阶梯水价，价目如右表（注：水费按月结算，m3表示立方米）：例：某户居民5月份共用水23m3，则应缴水费3×18+4×(23-18)=74（元）．

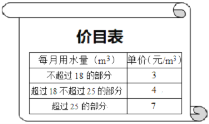
    （1）若A居民家1月份共用水12m3，则应缴水费__________元；

    （2）若B居民家2月份共缴水费66元，则用水__________m3；

    （3）若C居民家3月份用水量为am3（a低于20m3，即a<20)，且C居民家3、4两个月用水量共40m3，求3、4两个月共缴水费多少元？（用含a的代数式表示，不要求化简）

    （4）在（3）中，当a=19时，求C居民家3、4两个月共缴水费多少元？

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】（本题10分）为积极响应政府提出的“绿色发展低碳出行”号召，某自行车厂决定生产一批共享单车投入市场．该厂原计划一周生产1400辆共享单车，平均每天生产200辆，由于各种原因实际每天生产量与计划量相比有出入．下表是某周的生产情况（超产为正、减产为负）：

    　⑴根据记录可知前三天共生产　 　辆；

    　⑵产量最多的一天比产量最少的一天多生产　 　辆；

    　⑶该厂实行每周计件工资制，每生产一辆车可得60元，若超额完成任务，则超过部分每辆另奖15元；少生产一辆扣15元，那么该厂工人这一周的工资总额是多少？

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】已知在透明纸面上有一数轴(如图1)，折叠透明纸面．

    （1）若表示1的点与表示－1的点重合，则表示－7的点与表示 的点重合；

    （2）若表示－2的点与表示6的点重合，回答以下问题:

    ①表示12的点与表示 的点重合；

    ②如图2，若数轴上AB两点之间的距离为2020(点A在点B的左侧)，且AB两点经折叠后重合，则AB两点表示的数分别是 ．

    （3）如图3，若m和n表示的点C和点D经折叠后重合(m＞n)，折痕与数轴的交点为折痕点．已知线段CD上两点P、Q (点P在点Q的左侧，PQ＜CD)，PQ＝a．当线段PQ的端点与折痕点重合时，求PQ两点表示的数分别是多少?(用含m，n，a的代数式表示)．

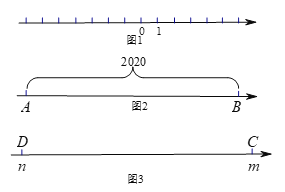
    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，在平面直角坐标系中，矩形OABC的顶点A、C的坐标分别为（10，0），（0，4），点D是OA的中点，点P在BC上运动，当△ODP是腰长为5的等腰三角形时，点P的坐标为______．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】（10分）如图，在平面直角坐标系中，反比例函数的图象和矩形ABCD在第二象限，AD平行于x轴，且AB=2，AD=4，点C的坐标为（﹣2，4）．

    （1）直接写出A、B、D三点的坐标；

    （2）若将矩形只向下平移，矩形的两个顶点恰好同时落在反比例函数的图象上，求反比例函数的解析式和此时直线AC的解析式y=mx+n．并直接写出满足的x取值范围．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】某年级380名师生秋游，计划租用7辆客车，现有甲、乙两种型号客车，它们的载客量和租金如表．

    甲种客车

    乙种客车

    载客量（座/辆）

    60

    45

    租金（元/辆）

    550

    450

    （1）设租用甲种客车x辆，租车总费用为y元．求出y（元）与x（辆）之间的函数表达式；

    （2）当甲种客车有多少辆时，能保障所有的师生能参加秋游且租车费用最少，最少费用是多少元？

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】一轮船在P处测得灯塔A在正北方向，灯塔B在南偏东30°方向，轮船向正东航行了900m，到达Q处，测得A位于北偏西60°方向， B位于南偏西30°方向．

    （1）线段BQ与PQ是否相等？请说明理由；

    （2）求A、B间的距离（结果保留根号）．

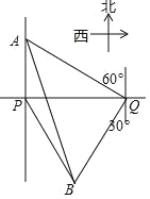
    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】“端午节”是我国的传统佳节，民间历来有吃“粽子”的习俗，某食品厂为了解市民对去年销售量较好的肉馅粽、豆沙粽、红枣粽、蛋黄馅粽（以下分别用A,B,C,D表示这四种不同口味粽子的喜爱情况，在节前对某居民区市民进行了抽样调查，并将调查结果绘制成如下两幅统计图．

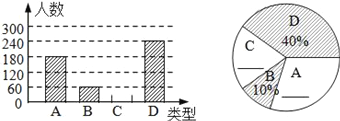
    请根据以上信息回答：

    （1）本次参加抽样调查的居民有多少人？将不完整的条形图和扇形图补充完整；

    （2）若居民区有8000人，请估计爱吃C ，D粽的总人数；

    （3）若有外型完全相同的A,B,C,D粽各一个煮熟后，小王吃了两个，用列表或画树状图的方法，求他第二个吃到的恰好是C粽的概率．

    查看答案和解析>>

    同步练习册答案