
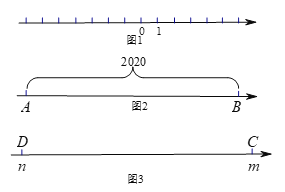
����Ŀ����֪����ֽ������һ����(��ͼ1)���۵���ֽ�森
��1������ʾ1�ĵ����ʾ��1�ĵ��غϣ����ʾ��7�ĵ����ʾ �ĵ��غϣ�
��2������ʾ��2�ĵ����ʾ6�ĵ��غϣ��ش���������:
�ٱ�ʾ12�ĵ����ʾ �ĵ��غϣ�
����ͼ2����������AB����֮��ľ���Ϊ2020(��A�ڵ�B�����)����AB���㾭�۵����غϣ���AB�����ʾ�����ֱ��� ��
��3����ͼ3����m��n��ʾ�ĵ�C�͵�D���۵����غ�(m��n)���ۺ�������Ľ���Ϊ�ۺ۵㣮��֪�߶�CD������P��Q (��P�ڵ�Q����࣬PQ��CD)��PQ��a�����߶�PQ�Ķ˵����ۺ۵��غ�ʱ����PQ�����ʾ�����ֱ��Ƕ���?(�ú�m��n��a�Ĵ���ʽ��ʾ)��
���𰸡���1��![]() ����2����-8����-1008 ��1012 ����3����PΪ�ۺ۵㣬��P:
����2����-8����-1008 ��1012 ����3����PΪ�ۺ۵㣬��P:![]() �� Q:
�� Q:![]() ����QΪ�ۺ۵㣬��P:
����QΪ�ۺ۵㣬��P:![]() �� Q:
�� Q:![]() .
.
��������
��1����������ʾ1�ĵ����ʾ��1�ĵ��غ����ҳ��Գ��ᣬ���ɵó��𰸣�
��2���ٸ�������ʾ��2�ĵ����ʾ6�ĵ��غ����ҳ��Գ��ᣬ���ɵó��𰸣��ڸ��ݶԳ���������Գ������Ϊ1010�ĵ㼴�ɵó��𰸣�
��3�����ݣ�2���ļ��㷽�����㼴�ɵó���.
�⣺��1��������ɵã�ԭ��Ϊ�Գ��ᣬ�ʴ�Ϊ��7 ��
��2����������ɵã�2Ϊ�Գ��ᣬ�ʴ�Ϊ��-8��
�ڡ߶Գ���Ϊ2
��2����Ϊ1010�ĵ�Ϊ��-1008��1012
�ֵ�A�ڵ�B�����
���A��ʾ����Ϊ-1008����B��ʾ����Ϊ1012��
��3����������ɵã��ۺ۵�Ϊ![]()
����PΪ�ۺ۵㣬��P:![]() ��Q:
��Q:![]()
����QΪ�ۺ۵㣺��P:![]() ��Q:
��Q:![]()


 ���Ŀ��ּ�����ҵ�����ҵ����������ϵ�д�
���Ŀ��ּ�����ҵ�����ҵ����������ϵ�д� ����ѵ��ϵ�д�
����ѵ��ϵ�д� ��ĩ�����ϵ�д�
��ĩ�����ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
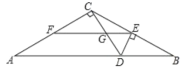
����Ŀ����ͼ����֪EF�ǡ�ABC����λ�ߣ�DE��BC��AB�ڵ�D��CD��EF���ڵ�G,��CD��AC,EF=8��EG=3����AC�ij�Ϊ___________.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ʾ��һ����Ϊ2m����Ϊ2n�ij����Σ���ͼ�������ü������ֳ��ĸ�С�����Σ�Ȼ��ͼ�ڵķ�ʽƴ��һ�������Σ�

��1������Ϊͼ���е���Ӱ���ֵ������εı߳�����_________________��
��2���������ֲ�ͬ�ķ����д���ʽ��ʾͼ������Ӱ���ֵ������
������ __________________�������� _____________________��
��3���۲�ͼ�ڣ�����д��(m+n)2��(m-n)2��mn����������ʽ֮��ĵ�����ϵ��
��________________________ .
��4�����ݣ�3�����еĵ�����ϵ������������⣺��a+b=6��ab=4������(a-b)2��ֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
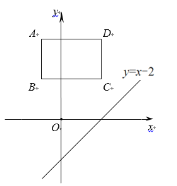
����Ŀ����ͼ���ı���ABCD�Ǿ��Σ�AD��![]() �ᣬ��B������Ϊ (-1��2)����D������Ϊ(2��4)����ֱ��y=x-2����ƽ��m����λ��ʹƽ�ƺ��ֱ��ǡ�þ�����D .
�ᣬ��B������Ϊ (-1��2)����D������Ϊ(2��4)����ֱ��y=x-2����ƽ��m����λ��ʹƽ�ƺ��ֱ��ǡ�þ�����D .
��1����m��ֵ��
��2��ƽ�ƺ��ֱ������εı�BC���ڵ�E�����CDE�����.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ѧУ�����У�һ�����ӿ���6�ˣ������������ְڷŷ�ʽ:
��1������5������ʱ����һ�ַ�ʽ���� �ˣ��ڶ��ַ�ʽ���� �ˣ�
��2������n������ʱ����һ�ַ�ʽ���� �ˣ��ڶ��ַ�ʽ���� �ˣ�
��3����ѧ����200����ѧУ�Ͳͣ�������ֻ��60�������IJ�������������ʦ�������ѡ���������ַ�ʽ���ڷŲ���?Ϊʲô?

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����������1��2016��һ���������������
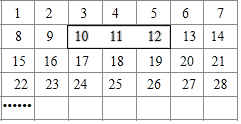
ƽ�Ʊ��д���Ӱ�ķ��������������ĺͿ����ǣ�������
A.2000B.2019C.2100D.2148
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����1�����㣨��![]() ����2��16�£���2��3+���Щ�tan60�㣩0��2
����2��16�£���2��3+���Щ�tan60�㣩0��2![]() cos30�㣻
cos30�㣻
��2���Ȼ�������ֵ��![]() ��
��![]() ��
��![]() ������x���㷽��x2+4x��5=0��
������x���㷽��x2+4x��5=0��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
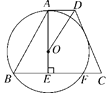
����Ŀ����ͼ������ABCD�У�AD��BC��AE��BC�ڵ�E����ADC��ƽ���߽�AE�ڵ�O���Ե�OΪԲ�ģ�OAΪ�뾶��Բ������B����BC����һ��F.
(1)��֤��CD���O���У�
(2)��BF��24��OE��5����tan��ABC��ֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
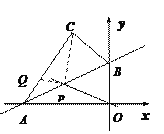
����Ŀ����ͼ,��ֱ֪��![]() ��x�ᡢy��ֱ���A, B���㣬����AOB��ֱ��AB���ۣ�ʹ��O���ڵ�C��, ��P��Q�ֱ���AB , AC��,��PC+PQȡ��Сֵʱ,ֱ��OP�Ľ���ʽΪ�� ��
��x�ᡢy��ֱ���A, B���㣬����AOB��ֱ��AB���ۣ�ʹ��O���ڵ�C��, ��P��Q�ֱ���AB , AC��,��PC+PQȡ��Сֵʱ,ֱ��OP�Ľ���ʽΪ�� ��
A. y=- ![]() B. y=-
B. y=- ![]() C. y=-
C. y=- ![]() D.
D. ![]()
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com