练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

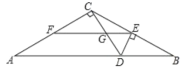
    【题目】如图，已知EF是△ABC的中位线，DE⊥BC交AB于点D，CD与EF交于点G,若CD⊥AC,EF=8，EG=3，则AC的长为___________.

    【答案】8

    【解析】

    由三角形中位线定理得出AB=2EF=16，EF∥AB，AF=CF，CE=BE，证出GE是△BCD的中位线，得出BD=2EG=6，AD=AB-BD=10，由线段垂直平分线的性质得出CD=BD=6，再由勾股定理即可求出AC的长．

    ∵EF是△ABC的中位线，

    ∴AB=2EF=16，EF∥AB，AF=CF，CE=BE，

    ∴G是CD的中点，

    ∴GE是△BCD的中位线，

    ∴BD=2EG=6，

    ∴AD=AB-BD=10，

    ∵DE⊥BC，CE=BE，

    ∴CD=BD=6，

    ∵CD⊥AC，

    ∴∠ACD=90°，

    ∴AC=；

    故答案为：8．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    【题目】已知四边形ABCD是正方形，△ADE是等边三角形，求∠BEC的度数．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】已知有理数．按要求完成下列各题．

    （1）请把题中各数填入相应的集合中：

    ①整数集合：{　 　…}

    ②负数集合：{　 　…}

    （2）把题中各数用数轴上的点表示出来，并用“＜“连接起来．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，将一条数轴在原点O和点B处各折一下，得到一条“折线数轴”．图中点A表示﹣10，点B表示10，点C表示18，我们称点A和点C在数轴上相距28个长度单位，动点P从点A出发，以2单位/秒的速度沿着“折线数轴”的正方向运动，从点O运动到点B期间速度变为原来的一半；点P从点A出发的同时，点Q从点C出发，以1单位/秒的速度沿着“折线数轴”的负方向运动，当点P到达B点时，点P、Q均停止运动．设运动的时间为t秒．问：

    （1）用含t的代数式表示动点P在运动过程中距O点的距离；

    （2）P、Q两点相遇时，求出相遇时间及相遇点M所对应的数是多少？

    （3）是否存在P、O两点在数轴上相距的长度与Q、B两点在数轴上相距的长度相等时？若存在，请直接写出t的取值；若不存在，请说明理由．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】（1）计算：．

    （2）如图，一次函数y=x+b与反比例函数在第一象限的图象交于点B，且点B的横坐标为1，过点B作y轴的垂线，C为垂足，若S△BCO= ，求一次函数和反比例函数的解析式．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

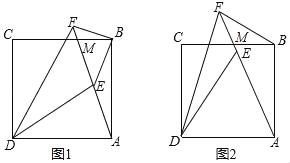
    【题目】如图，点M是正方形ABCD的边BC上一点，连接AM，点E是线段AM上一点，∠CDE的平分线交AM延长线于点F．

    (1)如图1，若点E为线段AM的中点，BM：CM＝1：2，BE＝，求AB的长；

    (2)如图2，若DA＝DE，求证：BF+DF＝AF．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】为充分发挥市场机制和价格杠杆在水资源配置中的作用，促进节约用水，提高用水效率，2017年7月1日起某地实行阶梯水价，价目如右表（注：水费按月结算，m3表示立方米）：例：某户居民5月份共用水23m3，则应缴水费3×18+4×(23-18)=74（元）．

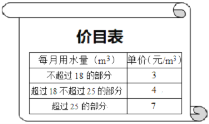
    （1）若A居民家1月份共用水12m3，则应缴水费__________元；

    （2）若B居民家2月份共缴水费66元，则用水__________m3；

    （3）若C居民家3月份用水量为am3（a低于20m3，即a<20)，且C居民家3、4两个月用水量共40m3，求3、4两个月共缴水费多少元？（用含a的代数式表示，不要求化简）

    （4）在（3）中，当a=19时，求C居民家3、4两个月共缴水费多少元？

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】观察表一，寻找规律，表二、表三、表四分别是从表一中截取的一部分，则a+b﹣m＝_____．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

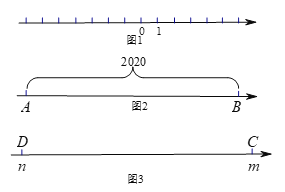
    【题目】已知在透明纸面上有一数轴(如图1)，折叠透明纸面．

    （1）若表示1的点与表示－1的点重合，则表示－7的点与表示 的点重合；

    （2）若表示－2的点与表示6的点重合，回答以下问题:

    ①表示12的点与表示 的点重合；

    ②如图2，若数轴上AB两点之间的距离为2020(点A在点B的左侧)，且AB两点经折叠后重合，则AB两点表示的数分别是 ．

    （3）如图3，若m和n表示的点C和点D经折叠后重合(m＞n)，折痕与数轴的交点为折痕点．已知线段CD上两点P、Q (点P在点Q的左侧，PQ＜CD)，PQ＝a．当线段PQ的端点与折痕点重合时，求PQ两点表示的数分别是多少?(用含m，n，a的代数式表示)．

    查看答案和解析>>

    同步练习册答案