
【题目】(1)计算:![]() .
.
(2)如图,一次函数y=x+b与反比例函数![]() 在第一象限的图象交于点B,且点B的横坐标为1,过点B作y轴的垂线,C为垂足,若S△BCO=
在第一象限的图象交于点B,且点B的横坐标为1,过点B作y轴的垂线,C为垂足,若S△BCO= ![]() ,求一次函数和反比例函数的解析式.
,求一次函数和反比例函数的解析式.

科目:初中数学 来源: 题型:
【题目】已知,矩形ABCD中,AB=4cm,BC=8cm,AC的垂直平分线EF分别交AD、BC于点E、F,垂足为O.
(1)如图1,连接AF、CE.求证四边形AFCE为菱形,并求AF的长;
(2)如图2,动点P、Q分别从A、C两点同时出发,沿△AFB和△CDE各边匀速运动一周.即点P自A→F→B→A停止,点Q自C→D→E→C停止.在运动过程中,
①已知点P的速度为每秒5cm,点Q的速度为每秒4cm,运动时间为t秒,当A、C、P、Q四点为顶点的四边形是平行四边形时,求t的值.
②若点P、Q的运动路程分别为a、b(单位:cm,ab≠0),已知A、C、P、Q四点为顶点的四边形是平行四边形,求a与b满足的数量关系式.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在矩形ABCD中,点F在边BC上,且AF=AD,过点D作DE⊥AF,垂足为点E。
(1)求证:DE=AB;
(2)以D为圆心,DE为半径作圆弧交AD于点G,若BF=FC=1,试求![]() 的长。
的长。

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图是一根起点为1的数轴,现有同学将它弯折,弯折后虚线上第一行的数是1,第二行的数是13,第三行的数是43,…,依此规律,第五行的数是( )

A. 183 B. 157 C. 133 D. 91
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图:在数轴上A点表示数a,B点示数b,C点表示数c,b是最小的正整数,且a,b满足![]() +(c-7)2=0.
+(c-7)2=0.
(1) a= ,b= ,c= .
(2) 若将数轴折叠,使得A点与C点重合,则点B与数 表示的点重合.
(3) 点A,B,C开始在数轴上运动,若点A以每秒1个单位长度的速度向左运动,同时,点B和点C分别以每秒2个单位长度和4个单位长度的速度向右运动,假设t秒钟过后,若点A与点B之间的距离表示为AB,点A与点C之间的距离表示为AC,点B与点C之间的距离表示为BC.则AB= ,AC= ,BC= .(用含t的代数式表示)
(4) 请问:3BC-2AB的值是否随着时间t的变化而改变? 若变化,请说明理由;若不变,请求其值.
![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知EF是△ABC的中位线,DE⊥BC交AB于点D,CD与EF交于点G,若CD⊥AC,EF=8,EG=3,则AC的长为___________.
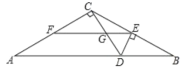
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一次函数y= ![]() x+6的图象与x轴、y轴分别交于A、B两点,点C与点A关于y轴对称.动点P、Q分别在线段AC、AB上(点P与点A、C不重合),且满足∠BPQ=∠BAO。
x+6的图象与x轴、y轴分别交于A、B两点,点C与点A关于y轴对称.动点P、Q分别在线段AC、AB上(点P与点A、C不重合),且满足∠BPQ=∠BAO。
(1)求点A、 B的坐标及线段BC的长度;
(2)当点P在什么位置时,△APQ≌△CBP,说明理由;
(3)当△PQB为等腰三角形时,求点P的坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,两个边长分别为a,b(a>b)的正方形连在一起,三点C,B,F在同一直线上,反比例函数y=![]() 在第一象限的图象经过小正方形右下顶点E.若OB2﹣BE2=10,则k的值是( )
在第一象限的图象经过小正方形右下顶点E.若OB2﹣BE2=10,则k的值是( )

A. 3 B. 4 C. 5 D. 4![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】学校餐厅中,一张桌子可坐6人,现有以下两种摆放方式:
(1)当有5张桌子时,第一种方式能坐 人,第二种方式能坐 人.
(2)当有n张桌子时,第一种方式能坐 人,第二种方式能坐 人.
(3)新学期有200人在学校就餐,但餐厅只有60张这样的餐桌,若你是老师,你打算选择以下哪种方式来摆放餐桌?为什么?

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com