
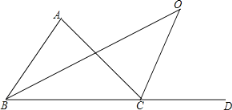
����Ŀ����֪������ABCD�У�AB=4cm��BC=8cm��AC�Ĵ�ֱƽ����EF�ֱ�AD��BC�ڵ�E��F������ΪO��
��1����ͼ1������AF��CE����֤�ı���AFCEΪ���Σ�����AF�ij���
��2����ͼ2������P��Q�ֱ��A��C����ͬʱ����������AFB����CDE���������˶�һ�ܣ�����P��A��F��B��Aֹͣ����Q��C��D��E��Cֹͣ�����˶������У�
����֪��P���ٶ�Ϊÿ��5cm����Q���ٶ�Ϊÿ��4cm���˶�ʱ��Ϊt�룬��A��C��P��Q�ĵ�Ϊ������ı�����ƽ���ı���ʱ����t��ֵ��
������P��Q���˶�·�̷ֱ�Ϊa��b����λ��cm��ab��0������֪A��C��P��Q�ĵ�Ϊ������ı�����ƽ���ı��Σ���a��b�����������ϵʽ��

���𰸡���1��֤����������AF=5cm��
��2������A��C��P��Q�ĵ�Ϊ������ı�����ƽ���ı���ʱ��![]() �룮
�룮
��a��b�����������ϵʽ��a+b=12��ab��0����
��������
��1����֤���ı���AFCEΪƽ���ı��Σ��ٸ��ݶԽ����ഹֱƽ�ֵ�ƽ���ı��������������ж������ݹ��ɶ����������AF�ij���
��2����������ۿ�֪����P����BF�ϡ�Q����ED��ʱ�����ܹ���ƽ���ı��Σ�����ƽ���ı��ε������г�������⼴��.
��1��֤�������ı���ABCD�Ǿ��Σ�
��AD��BC��
���CAD=��ACB����AEF=��CFE��
��EF��ֱƽ��AC������ΪO��
��OA=OC��
���AOE�ա�COF��
��OE=OF��
���ı���AFCEΪƽ���ı��Σ�
�֡�EF��AC��
���ı���AFCEΪ���Σ�
�����εı߳�AF=CF=xcm����BF=��8��x��cm��
��Rt��ABF��AB=4cm��
�ɹ��ɶ�����42+��8��x��2=x2��
���x=5��
��AF=5cm��
��2������Ȼ��P����AF��ʱ��Q����CD�ϣ���ʱA��C��P��Q�ĵ㲻���ܹ���ƽ���ı��Σ�
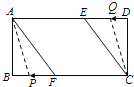
ͬ��P����AB��ʱ��Q����DE��CE�ϣ�Ҳ���ܹ���ƽ���ı��Σ�
���ֻ�е�P����BF�ϡ�Q����ED��ʱ�����ܹ���ƽ���ı��Σ�
����A��C��P��Q�ĵ�Ϊ������ı�����ƽ���ı���ʱ��PC=QA��
�ߵ�P���ٶ�Ϊÿ��5cm����Q���ٶ�Ϊÿ��4cm���˶�ʱ��Ϊt�룬
��PC=5t��QA=12��4t��
��5t=12��4t��
���![]() ��
��
����A��C��P��Q�ĵ�Ϊ������ı�����ƽ���ı���ʱ��![]() �룮
�룮
��������ã���A��C��P��Q�ĵ�Ϊ������ı�����ƽ���ı���ʱ����P��Q�ڻ���ƽ�еĶ�Ӧ���ϣ�
�����������
i����ͼ1����P����AF�ϡ�Q����CE��ʱ��AP=CQ����a=12��b����a+b=12��
ii����ͼ2����P����BF�ϡ�Q����DE��ʱ��AQ=CP����12��b=a����a+b=12��
iii����ͼ3����P����AB�ϡ�Q����CD��ʱ��AP=CQ����12��a=b����a+b=12��
����������a��b�����������ϵʽ��a+b=12��ab��0����



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ƽ��ֱ������ϵ�У��� A �� y ���������ϵ� B �� x �Ḻ�����ϣ��� AB=2����BAO=15������ P ���߶�OA �ϵ�һ�����㣬�� PB ![]() PA ����СֵΪ_____________��
PA ����СֵΪ_____________��

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ֱ��l��y=mx��m+1��mΪ��������m��0���������ύ��A��B���㣬����AOB��O��ԭ�㣩�����ǡΪ2�������Ҫ���ֱ��l�У� ��
A.1��
B.2��
C.3��
D.4��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
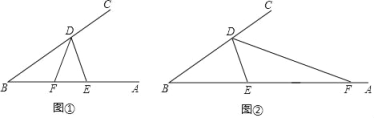
����Ŀ����֪��D��E�ֱ��ǡ�B������BC��BA�ϵĵ㣬��DEB��2��B��FΪBA��һ�㣮
��1����ͼ�٣���DFƽ�֡�BDE����֤��BD��DE+EF��
��2����ͼ�ڣ���DFΪ��DBE�����ƽ���ߣ�BD��DE��EF������������������ϵ����֤����Ľ��ۣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����A1��1��1����ֱ��y=x�ϣ�����A1�ֱ���y�ᡢx���ƽ���߽�ֱ��y= ![]() x�ڵ�B1 �� B2 �� ����B2��y���ƽ���߽�ֱ��y=x�ڵ�A2 �� ����A2��x���ƽ���߽�ֱ��y=
x�ڵ�B1 �� B2 �� ����B2��y���ƽ���߽�ֱ��y=x�ڵ�A2 �� ����A2��x���ƽ���߽�ֱ��y= ![]() x�ڵ�B3 �� �������մ˹��ɽ�����ȥ�����An�ĺ�����Ϊ ��
x�ڵ�B3 �� �������մ˹��ɽ�����ȥ�����An�ĺ�����Ϊ �� 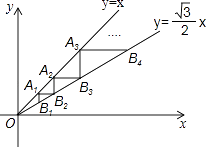
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��![]() ��
��![]() ����ǣ�
����ǣ�![]() ��
��![]() �Ľ�ƽ���߽��ڵ�
�Ľ�ƽ���߽��ڵ�![]() .
.
��1����![]() ��
��![]() ����
����![]() ��
��![]() ��
��
��2��̽��![]() ��
��![]() ��������ϵ����˵�����ɣ�
��������ϵ����˵�����ɣ�
��3����![]() ��
��![]() ����
����![]() �Ķ���.
�Ķ���.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���ܳ���ȵ��������Ρ����ı��Ρ��������ε����S3��S4��S6��Ĵ�С��ϵ�ǣ� ��
A.S3��S4��S6
B.S6��S4��S3
C.S6��S3��S4
D.S4��S6��S3
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ƽ��ֱ������ϵ�У������ɸ�������(�ᡢ�������Ϊ����)����˳��ͼ�з������У���(1��0)��(2��0)��(2��1)��(3��1)��(3��0)���� �����������̽���ɵã���50���������Ϊ�� ��
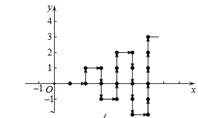
A. (10����5)B. (10����1) C. (10��0) D. (10��1��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��EF��AD,��1=��2,��BAC=70��.�����AGD�Ĺ�����д����.
�⣺ ��EF��AD,
���2=____(____________________________)
�֡ߡ�1=��2
���1=��3(��������)
��AB��_____(_____________________________)
���BAC+______=180��(___________________________)
�ߡ�BAC=70��
���AGD=_______��

�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com