Question

【题目】周长相等的正三角形、正四边形、正六边形的面积S3、S4、S6间的大小关系是（ ）
A.S3＞S4＞S6
B.S6＞S4＞S3
C.S6＞S3＞S4
D.S4＞S6＞S3

Answer 1

【答案】B
【解析】解：设正六边形的边长为a，如图所示，
则正△ABC的边长为2a，正方形ABCD的边长为 ．
如图（1），过A作AD⊥BC，D为垂足；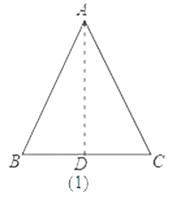

∵△ABC是等边三角形，BC=2a，
∴BD=a，由勾股定理得，AD= = = a，
∴S3=S△ABC= BCAD= ×2a× a= a2≈1.73a2 ．
如图（2），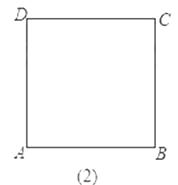

∵四边形ABCD是正方形，
∴AB= ，
∴S4=S□ABCD=AB2= × = a2≈2.25a2 ．
如图（3），过O作OG⊥BC，G为垂足，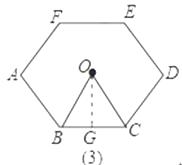

∵六边形ABCDEF是正六边形，
∴∠BOC= =60°，
∴∠BOG=30°，OG= = = a．
∴S△BOC= × a×a= a2 ，
∴S6=6S△BOC=6× a= a2≈2.59a2 ．
∵2.59a2＞2.25a2＞1.73a2 ．
∴S6＞S4＞S3 ．
故答案为：B．
根据正六边形的边长和半径相等，因此设正六边形的边长为a，再根据正六边形、正三角形、正方形的周长相等，用含a的代数式分别表示出正三角形和正方形的边长，然后分别求正六边形、正三角形、正方形的面积，比较它们的面积大小，即可得出答案。