
【题目】如图,已知AB∥CD,∠EBF=2∠ABE,∠EDF=2∠CDE,则∠E与∠F之间满足的数量关系是( )
A. ∠E=∠FB. ∠E+∠F=180°
C. 3∠E+∠F=360°D. 2∠E-∠F=90°
 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】周长相等的正三角形、正四边形、正六边形的面积S3、S4、S6间的大小关系是( )
A.S3>S4>S6
B.S6>S4>S3
C.S6>S3>S4
D.S4>S6>S3
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知⊙O的半径为2,点P是⊙O内一点,且OP= ![]() ,过P作互相垂直的两条弦AC、BD,则四边形ABCD面积的最大值为( )
,过P作互相垂直的两条弦AC、BD,则四边形ABCD面积的最大值为( )
A.4
B.5
C.6
D.7
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,EF∥AD,∠1=∠2,∠BAC=70°.将求∠AGD的过程填写完整.
解: ∵EF∥AD,
∴∠2=____(____________________________)
又∵∠1=∠2
∴∠1=∠3(等量代换)
∵AB∥_____(_____________________________)
∴∠BAC+______=180°(___________________________)
∵∠BAC=70°
∴∠AGD=_______.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC中,AB=AC,∠BAC=40°,将△ABC绕点A按逆时针方向旋转100°.得到△ADE,连接BD,CE交于点F.
(1)求证:△ABD≌△ACE;
(2)求证:四边形ABFE是菱形.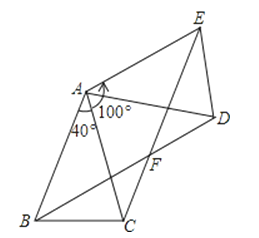
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知 ![]() 的三边长为a,b,c,且满足方程a2x2-(c2-a2-b2)x+b2=0,则方程根的情况是( )。
的三边长为a,b,c,且满足方程a2x2-(c2-a2-b2)x+b2=0,则方程根的情况是( )。
A.有两相等实根
B.有两相异实根
C.无实根
D.不能确定
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com