【题目】如图，将矩形ABCD绕点A顺时针旋转到矩形A′B′C′D′的位置，旋转角为α（0°＜α＜90°），若∠1=110°，则∠α= ．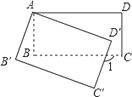
科目：初中数学 来源： 题型：
【题目】阅读下列一段文字：在直角坐标系中，已知两点的坐标是M（x1，y1），N（x2，y2）），M，N两点之间的距离可以用公式MN＝
计算．解答下列问题：
（1）若点P（2，4），Q（﹣3，﹣8），求P，Q两点间的距离；
（2）若点A（1，2），B（4，﹣2），点O是坐标原点，判断△AOB是什么三角形，并说明理由．
（3）已知点A(5，5)，B(-4，7)，点P在x轴上，且要使PA+PB的和最小，求PA+PB的最小值．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，在网格（每个小正方形的边长均为1）中选取9个格点（格线的交点称为格点），如果以A为圆心，r为半径画圆，选取的格点中除点A外恰好有3个在圆内，则r的取值范围为（ ）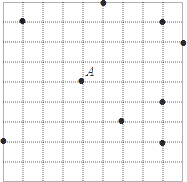
A.2 
＜r＜ 
B. ＜r≤3
C. ＜r＜5
D.5＜r＜ 
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，已知AB∥CD，∠EBF=2∠ABE，∠EDF=2∠CDE，则∠E与∠F之间满足的数量关系是（ ）
A. ∠E=∠FB. ∠E＋∠F=180°
C. 3∠E＋∠F=360°D. 2∠E-∠F=90°
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，在Rt△ABC中，∠C＝90°，点D是AB边中点，点E是BC边上一点，将△ADE沿DE折叠，得到△FDE，使△FDE与△BDE重叠部分的面积是△AEB面积的
，若AC＝3，BC＝6，则线段BE的长为__________．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，直线
与x轴、y轴分别相交于A、B两点，与直线
交于点C，且点C的横坐标为1．
（1）求b的值；
（2）点
，
在直线上，若
，则
__________
．
（3）若动点P在线段OC上（点P不与点C重合），连接PA，PB，设点P的横坐标为m，△PAB的面积为S，求S关于m的函数关系式（不要求写出自变量m的取值范围）．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】兴华商店准备购进甲、乙两种书包出售，每个甲种书包的进价比每个乙种书包的进价多20元，购进3个甲种书包的费用和购进4个乙种书包的费用相等，现计划购进两种书包共100个，其中乙种书包不少于35个．
（1）甲种书包进价为__________元/个，乙种书包进价为__________元/个；
（2）若甲种书包每个售价120元，乙种书包每个售价90元，且购进这100个书包的费用不低于7200元，如果这100个书包都可售完，那么兴华商店如何进货才能获得最大利润？最大利润是多少？
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】在菱形
中，
．
（1）如图1，点
为线段
的中点，连接
，
．若
，求线段
的长．
（2）如图2，
为线段
上一点（不与
，
重合），以
为边向上构造等边三角形
，线段
与
交于点
，连接
，
，
为线段的中点．连接
，
判断与的数量关系，并证明你的结论．
（3）在（2）的条件下，若
，请你直接写出
的最小值．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】阅读下面材料
已知：如图，四边形ABCD是平行四边形；
求作：菱形AECF，使点E，F分别在BC，AD上．
小凯的作法如下：
（1）连接AC；
（2）作AC的垂直平分线EF分别交BC，AD于E，F．
（3）连接AE，CF
所以四边形AECF是菱形．
老师说：“小凯的作法正确”．
回答问题：
已知：在平行四边形ABCD中，点E、F分别在边BC、AD上______________________________________________．（补全已知条件）
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
