
����Ŀ���˻��̵��������ס�������������ۣ�ÿ����������Ľ��۱�ÿ����������Ľ��۶�20Ԫ������3����������ķ��ú���4����������ķ�����ȣ��ּƻ��������������100���������������������35����
��1�������������Ϊ__________Ԫ/���������������Ϊ__________Ԫ/����
��2�����������ÿ���ۼ�120Ԫ���������ÿ���ۼ�90Ԫ���ҹ�����100������ķ��ò�����7200Ԫ�������100������������꣬��ô�˻��̵���ν������ܻ�����������������Ƕ��٣�
���𰸡���1��80��60����2���������Ϊ3650����ʱӦ��65���������35�������
��������
��1����������Ľ���xԪ/�����������Ľ���Ϊ(x+20)Ԫ/�������������з��̼��ɽ��
��2�����������г�����ʽ�飬���m��ȡֵ��Χ�����г�w�ı���ʽ���ۼ��ɣ�
��1����������Ľ���ΪxԪ/�����������Ľ���Ϊ(x+20)Ԫ/������������ã�3(x+20)=4x�����x=60��
�����������Ϊ80Ԫ/�������������Ϊ60Ԫ/����
��2����ƻ�����m�������������(100-m)�����������������ã�

��ã�60��m��65��
��������ΪwԪ��
��w=��120-80��m+(90-60)(100-m)=10m+3000��
���Ե�m=65ʱ��w�����ֵ�����ֵΪ3650��
��ʱӦ��65���������35���������



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��ֱ��y����2x+4��x�ᡢy��ֱ���A��B���㣬P��ֱ��AB�ϵ�һ�����㣬��C������Ϊ����4��0����PC��y�����D��O��ԭ�㣮
��1�����AOB�������
��2���߶�AB�ϴ���һ��P��ʹ��DOC�ա�AOB�����ʱ��P�����ꣻ
��3��ֱ��AB�ϴ���һ��P��ʹ��P��C��OΪ�����������������AOB�����ȣ����P������꣮

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����һ�����ǰ�ƴ����ͼ��ʾ��ͼ�Σ�����C��CFƽ����DCE��DE�ڵ�F��

��1����֤��CF��AB��
��2������DFC�Ķ�����
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��������ABCD�Ƶ�A˳ʱ����ת������A��B��C��D���λ�ã���ת��Ϊ����0�㣼����90�㣩������1=110�㣬��Ϧ�= ��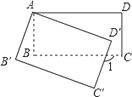
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������ʦ��ѧ������һ���⣺
��(2a+b)(2a��b)+2(2a��b)2+(2ab2��16a2b)��(��2a)��ֵ������a��![]() ��b����1��ͬѧ�ǿ�����Ŀ����ͬ�Ŀ�����С��˵������b����1�Ƕ���ģ���С��˵������������������Ͳ��������������Բ����࣮��
��b����1��ͬѧ�ǿ�����Ŀ����ͬ�Ŀ�����С��˵������b����1�Ƕ���ģ���С��˵������������������Ͳ��������������Բ����࣮��
(1)����Ϊ����˭˵���е�����Ϊʲô��
(2)��xm���ڱ��}����Ľ��������x2m��ֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ABC�У�AB=AC����BAC=40�㣬����ABC�Ƶ�A����ʱ�뷽����ת100�㣮�õ���ADE������BD��CE���ڵ�F��
��1����֤����ABD�ա�ACE��
��2����֤���ı���ABFE�����Σ�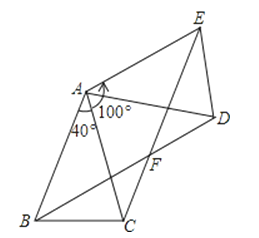
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ABC�������������ֱ�ΪA��1��1����B��4��2����C��3��4���� 
�ٻ�����ABC����ƽ��5����λ���Ⱥ�õ��ġ�A1B1C1��
���뻭����ABC����ԭ��ԳƵġ�A2B2C2 �� ��д����A2��B2��C2���ꣻ
���뻭����ABC��ԭ��O��ʱ����ת90����A3B3C3 �� ��д����A3��B3��C3���꣮
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ�������Ե�OΪԲ�ĵ�ͬ��Բ��
ͼ1 ͼ2
��1����ͼ1����Բ����AB��СԲ��C��D���㣬���ж�AC��BD��������ϵ����˵������.
��2����ͼ2������Բ����AB����ƽ��ʹ��ΪСԲ�����ߣ��е�ΪC��֤����AC=BC.
��3���ڣ�2���Ļ����ϣ���֪AB=20cm��ֱ��д��Բ�������.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��ABΪ��ԲO��ֱ����CΪBA�ӳ�����һ�㣬CD�а�ԲO�ڵ�D������OD����BE��CD�ڵ�E������ԲO�ڵ�F����֪CE=12��BE=9
��1����֤����COD�ס�CBE��
��2�����ԲO�İ뾶 ![]() �ij�
�ij�
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com