
【题目】如图,直线y=﹣2x+4与x轴、y轴分别交于A、B两点,P是直线AB上的一个动点,点C的坐标为(﹣4,0),PC交y轴点于D,O是原点.
(1)求△AOB的面积;
(2)线段AB上存在一点P,使△DOC≌△AOB,求此时点P的坐标;
(3)直线AB上存在一点P,使以P、C、O为顶点的三角形面积与△AOB面积相等,求出P点的坐标.

【答案】(1)△AOB的面积是4;(2)点P的坐标是(![]() ,
,![]() );(3)点P的坐标为:(1,2)或(3,﹣2).
);(3)点P的坐标为:(1,2)或(3,﹣2).
【解析】
(1)利用直线解析式易求得点A、B的坐标,从而得到线段OA=2,OB=4.所以根据直角三角形的面积公式来求△AOB的面积;
(2)根据全等三角形的对应边相等求得线段OD=OA=2,则易求点D的坐标.由点C、D的坐标易求得直线CD的方程,则点P是直线CD与直线AB的交点;
(3)设P(x,y).根据点C的坐标易求得线段OC=4.所以由直角三角形的面积公式列出关于y的方程,通过解方程可以求得点P的坐标.
解:(1)如图1,∵直线y=﹣2x+4与x轴、y轴分别相交于A、B两点,
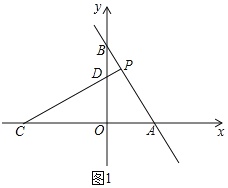
∴A(2,0),B(0,4),
∴OA=2,OB=4.
∴SAOB=![]() OAOB=
OAOB=![]() ×2×4=4,即△AOB的面积是4;
×2×4=4,即△AOB的面积是4;
(2)∵△DOC≌△AOB,
∴OD=OA=2,
∴D(0,2).
故设直线CD的解析式为y=kx+2(k≠0).
∵C(﹣4,0)
则0=﹣4k+2,
解得,k=![]() ,
,
∴直线CD的解析式为y=![]() x+2.
x+2.
又∵点P是直线CD与直线AB的交点,
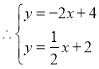
解得: 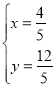
![]() 点
点 ![]() 的坐标是
的坐标是 ![]()
(3)如图2,设P(x,y),
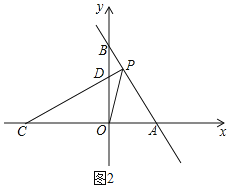
又∵点C的坐标为(﹣4,0),
∴OC=4,
∵S△COP=S△AOB,
∴![]() OC×|y|=4,即|y|=2,
OC×|y|=4,即|y|=2,
解得,y=±2,
∵P是直线AB上一点,
∴点P的坐标为:(1,2)或(3,﹣2).


 捷径训练检测卷系列答案
捷径训练检测卷系列答案 小夫子全能检测系列答案
小夫子全能检测系列答案科目:初中数学 来源: 题型:
【题目】阅读理解:已知点P(x0 , y0)和直线y=kx+b,则点P到直线y=kx+b的距离,可用公式d= ![]() 计算.
计算.
例如:求点P(﹣1,2)到直线y=3x+7的距离.
解:因为直线y=3x+7,其中k=3,b=7.
所以点P(﹣1,2)到直线y=3x+7的距离为:d= ![]() =
= ![]() =
= ![]() =
= ![]() .
.
根据以上材料,解答下列问题:
(1)求点P(1,﹣1)到直线y=x﹣1的距离;
(2)已知⊙Q的圆心Q坐标为(0,5),半径r为2,判断⊙Q与直线y= ![]() x+9的位置关系并说明理由;
x+9的位置关系并说明理由;
(3)已知直线y=﹣2x+4与y=﹣2x﹣6平行,求这两条直线之间的距离.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】上周六,小明一家共7人从某地出发去参观世博会.小明提议:让爸爸载着爷爷、奶奶、外公、外婆去,自己和妈妈从某41路车去,最后在地铁8号线某博物馆汇合,图中![]() 分别表示某41路车与小轿车在行驶中的路程(千米)与时间(分钟)关系,试观察图像并回答下列问题:
分别表示某41路车与小轿车在行驶中的路程(千米)与时间(分钟)关系,试观察图像并回答下列问题:

(1)某41路车在途中行驶的平均速度为 千米/分钟;此次行驶的路程是 千米;
(2)写出小轿车在行驶过程中![]() 与
与![]() 的函数关系式: ,定义域为 ;
的函数关系式: ,定义域为 ;
(3)小明和妈妈乘坐的某41路出发 分钟后被爸爸的小轿车追上了.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读下列一段文字:在直角坐标系中,已知两点的坐标是M(x1,y1),N(x2,y2)),M,N两点之间的距离可以用公式MN=![]() 计算.解答下列问题:
计算.解答下列问题:

(1)若点P(2,4),Q(﹣3,﹣8),求P,Q两点间的距离;
(2)若点A(1,2),B(4,﹣2),点O是坐标原点,判断△AOB是什么三角形,并说明理由.
(3)已知点A(5,5),B(-4,7),点P在x轴上,且要使PA+PB的和最小,求PA+PB的最小值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知直线y=x与反比例函数y=![]() (x>0)图象交于A,过点A作AC⊥x轴,垂足为C,一次函数y=kx+b的图象经过点A,与y轴的正半轴交于B.
(x>0)图象交于A,过点A作AC⊥x轴,垂足为C,一次函数y=kx+b的图象经过点A,与y轴的正半轴交于B.
(1)求点A的坐标;
(2)若四边形ABOC的面积为3,求一次函数y=kx+b的表达式.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列说法正确的是( )
A.平移不改变图形的形状和大小,而旋转则改变图形的形状和大小
B.平移和旋转的共同点是改变了图形的位置,而图形的形状大小没有变化
C.图形可以向某方向平移一定距离,也可以向某方向旋转一定距离
D.在平移和旋转图形中,对应角相等,对应线段相等且平行
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某中学为了绿化校园,计划购买一批榕树和香樟树,经市场调查,榕树的单价比香樟树少20元,购买3棵榕树和2棵香樟树共需340元.
(1)榕树和香樟树的单价各是多少?
(2)根据学校实际情况,需购买两种树苗共150棵,总费用不超过10840元,且购买香樟树的棵数不少于榕树的1.5倍,请你算算该校本次购买榕树和香樟树共有哪几种方案.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在网格(每个小正方形的边长均为1)中选取9个格点(格线的交点称为格点),如果以A为圆心,r为半径画圆,选取的格点中除点A外恰好有3个在圆内,则r的取值范围为( )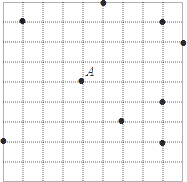
A.2 ![]() <r<
<r< ![]()
B.![]() <r≤3
<r≤3 ![]()
C.![]() <r<5
<r<5
D.5<r< ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】兴华商店准备购进甲、乙两种书包出售,每个甲种书包的进价比每个乙种书包的进价多20元,购进3个甲种书包的费用和购进4个乙种书包的费用相等,现计划购进两种书包共100个,其中乙种书包不少于35个.
(1)甲种书包进价为__________元/个,乙种书包进价为__________元/个;
(2)若甲种书包每个售价120元,乙种书包每个售价90元,且购进这100个书包的费用不低于7200元,如果这100个书包都可售完,那么兴华商店如何进货才能获得最大利润?最大利润是多少?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com