
【题目】如图,已知直线y=x与反比例函数y=![]() (x>0)图象交于A,过点A作AC⊥x轴,垂足为C,一次函数y=kx+b的图象经过点A,与y轴的正半轴交于B.
(x>0)图象交于A,过点A作AC⊥x轴,垂足为C,一次函数y=kx+b的图象经过点A,与y轴的正半轴交于B.
(1)求点A的坐标;
(2)若四边形ABOC的面积为3,求一次函数y=kx+b的表达式.

 能力评价系列答案
能力评价系列答案 唐印文化课时测评系列答案
唐印文化课时测评系列答案科目:初中数学 来源: 题型:
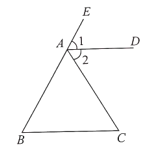
【题目】根据图形及题意填空,并在括号里写上理由.
己知:如图,![]() ,
,![]() 平分
平分![]() .
.
试说明:![]() .
.
解:因为![]() 平分
平分![]() (已知)
(已知)
所以![]() (角平分线的定义)
(角平分线的定义)
因为![]() (已知)
(已知)
所以∠_________=∠__________(________)
∠____________=∠_________(___________)
所以![]() .
.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读材料:
在平面直角坐标系xOy中,点P(x0 , y0)到直线Ax+By+C=0的距离公式为:d= ![]() .
.
例如:求点P0(0,0)到直线4x+3y﹣3=0的距离.
解:由直线4x+3y﹣3=0知,A=4,B=3,C=﹣3,
∴点P0(0,0)到直线4x+3y﹣3=0的距离为d= ![]() =
= ![]() .
.
根据以上材料,解决下列问题:
(1)点P1(3,4)到直线y=﹣ ![]() x+
x+ ![]() 的距离为;
的距离为;
(2)已知:⊙C是以点C(2,1)为圆心,1为半径的圆,⊙C与直线y=﹣ ![]() x+b相切,求实数b的值;
x+b相切,求实数b的值;
(3)如图,设点P为问题2中⊙C上的任意一点,点A,B为直线3x+4y+5=0上的两点,且AB=2,请求出S△ABP的最大值和最小值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】数学活动课上,张老师说:“![]() 是无理数,无理数就是无限不循环小数,同学们,你能把
是无理数,无理数就是无限不循环小数,同学们,你能把![]() 的小数部分全部写出来吗?”大家议论纷纷,晶晶同学说:“要把它的小数部分全部写出来是非常难的,但我们可以用(
的小数部分全部写出来吗?”大家议论纷纷,晶晶同学说:“要把它的小数部分全部写出来是非常难的,但我们可以用(![]() ﹣1)表示它的小数部分.”张老师说:“晶晶同学的说法是正确的,因为1<2<4,所以1<
﹣1)表示它的小数部分.”张老师说:“晶晶同学的说法是正确的,因为1<2<4,所以1<![]() <2,所以
<2,所以![]() 的整数部分是1,将这个数减去其整数部分,差就是小数部分.”亮亮说:“既然如此,因为2<
的整数部分是1,将这个数减去其整数部分,差就是小数部分.”亮亮说:“既然如此,因为2<![]() <3,所以
<3,所以![]() 的小数部分就是(
的小数部分就是(![]() ﹣2)了.”张老师说:“亮亮真的很聪明.”接着,张老师出示了一道练习题:“已知8+
﹣2)了.”张老师说:“亮亮真的很聪明.”接着,张老师出示了一道练习题:“已知8+![]() =x+y,其中x是一个整数,且0<y<1,请你求出2x+(
=x+y,其中x是一个整数,且0<y<1,请你求出2x+(![]() ﹣y)2019的值”.请同样聪明的你给出正确答案.
﹣y)2019的值”.请同样聪明的你给出正确答案.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读下面的推理过程,在括号内填上推理的依据,如图:

∵∠1+∠2=180°,∠2+∠4=180°(已知)
∴∠1=∠4( )
∴c∥a( )
又∵∠2+∠3=180°(已知 )
∠3=∠6( )
∴∠2+∠6=180°( )
∴a∥b( )
∴c∥b( )
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线y=﹣2x+4与x轴、y轴分别交于A、B两点,P是直线AB上的一个动点,点C的坐标为(﹣4,0),PC交y轴点于D,O是原点.
(1)求△AOB的面积;
(2)线段AB上存在一点P,使△DOC≌△AOB,求此时点P的坐标;
(3)直线AB上存在一点P,使以P、C、O为顶点的三角形面积与△AOB面积相等,求出P点的坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在等边△ABC中,D是边AC上一点,连接BD,将△BCD绕点B逆时针旋转60°,得到△BAE,连接ED,若BC=5,BD=4,则以下四个结论中: ①△BDE是等边三角形; ②AE∥BC; ③△ADE的周长是9; ④∠ADE=∠BDC.其中正确的序号是( )
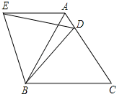
A.②③④B.①②④C.①②③D.①③④
查看答案和解析>>
科目:初中数学 来源: 题型:
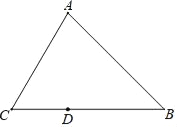
【题目】如图,已知△ABC中,∠ABC=45°,点D是BC边上一动点(与点B,C不重合),点E与点D关于直线AC对称,连结AE,过点B作BF⊥ED的延长线于点F.
(1)依题意补全图形;
(2)当AE=BD时,用等式表示线段DE与BF之间的数量关系,并证明.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】王老师给学生出了一道题:
求(2a+b)(2a﹣b)+2(2a﹣b)2+(2ab2﹣16a2b)÷(﹣2a)的值,其中a=![]() ,b=﹣1,同学们看了题目后发表不同的看法.小张说:条件b=﹣1是多余的.”小李说:“不给这个条件,就不能求出结果,所以不多余.”
,b=﹣1,同学们看了题目后发表不同的看法.小张说:条件b=﹣1是多余的.”小李说:“不给这个条件,就不能求出结果,所以不多余.”
(1)你认为他们谁说的有道理?为什么?
(2)若xm等于本題计算的结果,试求x2m的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com