
【题目】阅读下面的推理过程,在括号内填上推理的依据,如图:

∵∠1+∠2=180°,∠2+∠4=180°(已知)
∴∠1=∠4( )
∴c∥a( )
又∵∠2+∠3=180°(已知 )
∠3=∠6( )
∴∠2+∠6=180°( )
∴a∥b( )
∴c∥b( )
【答案】见解析
【解析】
依据同角的补角相等可证明∠1=∠4,依据平行线的判定定理可证明a∥c,依据对顶角的性质和等量代换可证明∠2+∠6=180°,最后依据平行线的判定定理和平行公理的推论进行证明即可.
因为∠1+∠2=180°,∠2+∠4=180°(已知),
所以∠1=∠4,(同角的补角相等)
所以a∥c.(内错角相等,两直线平行)
又因为∠2+∠3=180°(已知)
∠3=∠6(对顶角相等)
所以∠2+∠6=180°,(等量代换)
所以a∥b.(同旁内角互补,两直线平行)
所以c∥b.(平行与同一条直线的两条直线平行).
故答案为:同角的补角相等;内错角相等,两直线平行;对顶角相等;等量代换;同旁内角互补,两直线平行;平行与同一条直线的两条直线平行.


科目:初中数学 来源: 题型:
【题目】如图,AB是⊙O的直径,点C是⊙O上一点,AD与过点C的切线垂直,垂足为点D,直线DC与AB的延长线相交于点P,CE平分∠ACB,交AB于点E.
(1)求证:AC平分∠DAB;
(2)求证:△PCE是等腰三角形.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图①,一个正方体铁块放置在圆柱形水槽内,现以一定的速度往水槽中注水,28s时注满水槽.水槽内水面的高度y(cm)与注水时间x(s)之间的函数图象如图②所示.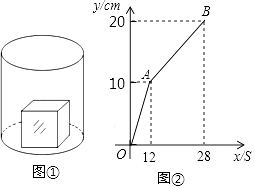
(1)正方体的棱长为cm;
(2)求线段AB对应的函数解析式,并写出自变量x的取值范围;
(3)如果将正方体铁块取出,又经过t(s)恰好将此水槽注满,直接写出t的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
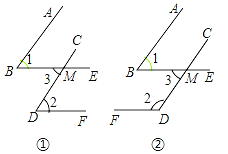
【题目】已知一个角的两边与另一个角的两边分别平行,请结合图,探索这两个角之间的关系,并说明理由.
(1)如图①,AB∥CD,BE∥DF,∠1与∠2的关系是 ;
证明:
(2)如图②,AB∥CD,BE∥DF,∠1与∠2的关系是 ;
证明:
(3)经过上述证明,我们可得出结论,如果一个角的两边与另一个角的两边分别平行,那么这两个角 ;
(4)若这两个角的两边分别平行,且一个角比另一个角的3倍少60°,则这两个角分别是多少度?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知直线y=x与反比例函数y=![]() (x>0)图象交于A,过点A作AC⊥x轴,垂足为C,一次函数y=kx+b的图象经过点A,与y轴的正半轴交于B.
(x>0)图象交于A,过点A作AC⊥x轴,垂足为C,一次函数y=kx+b的图象经过点A,与y轴的正半轴交于B.
(1)求点A的坐标;
(2)若四边形ABOC的面积为3,求一次函数y=kx+b的表达式.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,⊙O半径为4cm,其内接正六边形ABCDEF,点P,Q同时分别从A,D两点出发,以1cm/s速度沿AF,DC向终点F,C运动,连接PB,QE,PE,BQ.设运动时间为t(s).
(1)求证:四边形PEQB为平行四边形;
(2)填空:
①当t=s时,四边形PBQE为菱形;
②当t=s时,四边形PBQE为矩形.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某学校为了改善办学条件,计划购置一电子白板和一批笔记本电脑,经投标,购买一块电子白板比买三台笔记本电脑多3000元,购买4块电子白板和5台笔记本电脑共需80000元.
(1)求购买一块电子白板和一台笔记本电脑各需多少元?
(2)根据该校实际情况需购买电子白板和笔记本电脑的总数为396台,要求购买的总费用不超过2700000元,并购买笔记本电脑的台数不超过购买电子白板数量的3倍,该校有哪几种购买方案?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,正方形ABCD,点E在CD上,连接AE,BD,点G是AE中点,过点G作FH⊥AE,FH分别交AD,BC于点F,H,FH与BD交于点K,且HK=2FG,若EG=![]() ,则线段AF的长为_______________.
,则线段AF的长为_______________.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com