
【题目】如图,正方形ABCD,点E在CD上,连接AE,BD,点G是AE中点,过点G作FH⊥AE,FH分别交AD,BC于点F,H,FH与BD交于点K,且HK=2FG,若EG=![]() ,则线段AF的长为_______________.
,则线段AF的长为_______________.

【答案】![]()
【解析】
本题的解题关键是根据圆周角定理得出GK=EG,得到这个条件以后,再通过作辅助线,得到△MFH≌△ADE,得出FH的长,然后再根据已知计算即可.
如图,过H点向AD边做垂线,交AD于点M,
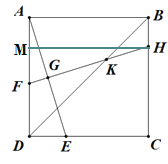
由题可知HM=AD,∠FMH=∠ADE=90°,
∵FH⊥AE,
∴∠FAG+∠AFG=90°,
∵∠ADE=90°,
∴∠FAG+∠AED=90°,
∴∠AED=∠AFG
∴△MFH≌△ADE,
∴FH=AE,
∵点G是AE中点,EG=![]() ,
,
∴FH=AE=![]()
由已知可得∠KDE=45°=![]() ∠HEG,
∠HEG,
∴点K位于以G点为圆心,以AE为直径的圆上,
∴AG=GK=EG=![]() ,
,
∴FG+HK=![]()
∵HK=2FG,
∴FG=![]() ,
,
根据勾股定理可得AF=![]() ,
,
故答案为:![]() .
.


科目:初中数学 来源: 题型:
【题目】阅读下面的推理过程,在括号内填上推理的依据,如图:

∵∠1+∠2=180°,∠2+∠4=180°(已知)
∴∠1=∠4( )
∴c∥a( )
又∵∠2+∠3=180°(已知 )
∠3=∠6( )
∴∠2+∠6=180°( )
∴a∥b( )
∴c∥b( )
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,∠1=∠2,∠C=∠D。
求证:∠A=∠F。
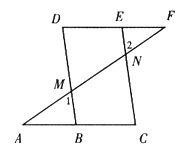
证明:∵∠1=∠2(已知),
又∠1=∠DMN(_______________),
∴∠2=∠_________(等量代换),
∴DB∥EC( ),
∴∠DBC+∠C=1800(两直线平行 , ),
∵∠C=∠D( ),
∴∠DBC+ =1800(等量代换),
∴DF∥AC( ,两直线平行),
∴∠A=∠F( )
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,OA=8,OB=6,C点与A点关于直线OB对称,动点P、Q分别在线段AC、AB上(点P不与点A.C重合),满足∠BPQ=∠BAO.
(1)当OP=_______时,△APQ≌△CBP,说明理由;
(2)当△PQB为等腰三角形时,求OP的长度.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,抛物线y=ax2+bx+c(a,b,c是常数,a>0)的部分图象如图所示,直线x=1是它的对称轴.若一元二次方程ax2+bx+c=0的一个根x1的取值范围是2<x1<3,则它的另一个根x2的取值范围是 . 
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】王老师给学生出了一道题:
求(2a+b)(2a﹣b)+2(2a﹣b)2+(2ab2﹣16a2b)÷(﹣2a)的值,其中a=![]() ,b=﹣1,同学们看了题目后发表不同的看法.小张说:条件b=﹣1是多余的.”小李说:“不给这个条件,就不能求出结果,所以不多余.”
,b=﹣1,同学们看了题目后发表不同的看法.小张说:条件b=﹣1是多余的.”小李说:“不给这个条件,就不能求出结果,所以不多余.”
(1)你认为他们谁说的有道理?为什么?
(2)若xm等于本題计算的结果,试求x2m的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】 学校“百变魔方”社团准备购买A,B两种魔方,已知购买2个A种魔方和6个B种魔方共需130元,购买3个A种魔方和4个B种魔方所需款数相同.

(1)求这两种魔方的单价;
(2)结合社员们的需求,社团决定购买A,B两种魔方共100个.某商店有两种优惠活动,如图所示.请根据以上信息,购进A种魔方多少个时,两种活动费用相同?
查看答案和解析>>
科目:初中数学 来源: 题型:
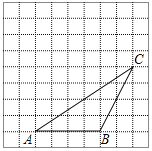
【题目】如图,在每个小正方形边长为1的方格纸中,△ADC的顶点都在方格纸格点上,将△ABC向左平移1格.再向上平移1格,
(1)在图中画出平移后的△A′B′C′;
(2)画出AB边上的高CE;
(3)过点A画BC的平行线;
(4)在图中,若△BCQ的面积等于△BCA的面积.则图中满足条件且异于点A的个点Q共有_____个.(注:格点指网格线的交点)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知AB是⊙O的直径,BC是⊙O的切线,B为切点,OC平行于弦AD,连接CD。过点D作DE⊥AB于E,交AC于点P,求证:点P平分线段DE。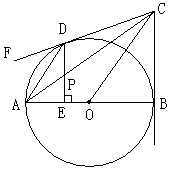
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com