
【题目】如图,在△ABC中,OA=8,OB=6,C点与A点关于直线OB对称,动点P、Q分别在线段AC、AB上(点P不与点A.C重合),满足∠BPQ=∠BAO.
(1)当OP=_______时,△APQ≌△CBP,说明理由;
(2)当△PQB为等腰三角形时,求OP的长度.

【答案】(1)2,理由见解析;(2)OP2或![]() .
.
【解析】
(1)求出∠PAQ=∠BCP,∠AQP=∠BPC,根据点的坐标求出AP=BC,根据全等三角形的判定推出即可.
(2)分为三种情况:①PQ=BP,②BQ=QP,③BQ=BP,根据(2)即可推出①,根据三角形外角性质即可判断②,根据勾股定理得出方程,即可求出③.
解:(1)当OP=2时,△APQ≌△CBP.
理由如下:
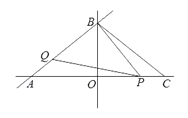
∵OA=8,OB=6,C点与A点关于直线OB对称,
∴![]() ,
,
∵OA=8,OP=2,
∴AP=BC=10
∵C点与A点关于直线OB对称,
∴∠BAO=∠BCO
∵∠BPQ=∠BAO,
∴∠BPQ=∠BCO
∵∠APB=∠APQ+∠BPQ=∠BCO+∠CBP,
∴∠APQ=∠CBP
在△APQ和△CBP中
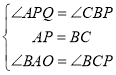 ,
,
∴△APQ≌△CBP(ASA)
(2)分为3种情况:
①当PB=PQ时,
由(1)得:△APQ≌△CBP时,PB=PQ此时OP=2;
②当BQ=BP时,
∠BPQ=∠BQP
∵∠BPQ=∠BAO,
∴∠BAO=∠BQP
根据三角形外角性质得:∠BQP>∠BAO,
∴这种情况不存在;
③当QB=QP时,
∠QBP=∠BPQ=∠BAO,
∴PB=PA,
设OP=x,则PB=PA=x+8
在Rt△OBP中,PB2=OP2+OB2,
∴(8+x)2=x2+62
解得:x![]() ;
;
∵点P在AC上,
∴点P在点O左边,
此时OP![]() ;
;
∴当△PQB为等腰三角形时,OP2或![]() ;
;


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
【题目】某学校为了改善办学条件,计划购置一电子白板和一批笔记本电脑,经投标,购买一块电子白板比买三台笔记本电脑多3000元,购买4块电子白板和5台笔记本电脑共需80000元.
(1)求购买一块电子白板和一台笔记本电脑各需多少元?
(2)根据该校实际情况需购买电子白板和笔记本电脑的总数为396台,要求购买的总费用不超过2700000元,并购买笔记本电脑的台数不超过购买电子白板数量的3倍,该校有哪几种购买方案?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在Rt△ABC中,∠ACB=90°,AC=8,BC=6,点D是以点A为圆心4为半径的圆上一点,连接BD,点M为BD中点,线段CM长度的最大值为 . 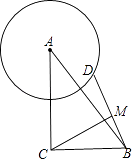
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列命题:①两条直线相交,一个角的两邻补角相等,则这两条直线垂直;②同位角相等;③点(5,6)与点(6,5)表示同一点;④若两个同旁内角互补,则它们的角平分线互相垂直;⑤点(![]() ,5)在第二象限.其中假命题的个数为( )
,5)在第二象限.其中假命题的个数为( )
A. 4B. 3C. 2D. 1
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠C=90°,点D是AB边中点,点E是BC边上一点,将△ADE沿DE折叠,得到△FDE,使△FDE与△BDE重叠部分的面积是△AEB面积的![]() ,若AC=3,BC=6,则线段BE的长为__________.
,若AC=3,BC=6,则线段BE的长为__________.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,正方形ABCD,点E在CD上,连接AE,BD,点G是AE中点,过点G作FH⊥AE,FH分别交AD,BC于点F,H,FH与BD交于点K,且HK=2FG,若EG=![]() ,则线段AF的长为_______________.
,则线段AF的长为_______________.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】四边形ABCD中,∠A=100°,∠C=70°.点M,N分别在AB,BC上,将△BMN沿MN翻折,得△FMN.若MF∥AD,FN∥DC,则∠D=_____°.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com