
【题目】在Rt△ABC中,∠ACB=90°,AC=8,BC=6,点D是以点A为圆心4为半径的圆上一点,连接BD,点M为BD中点,线段CM长度的最大值为 . 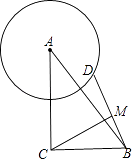
 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
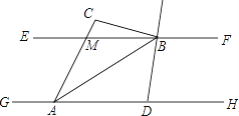
【题目】如图,已知EF∥GH,A、D为GH上的两点,M、B为EF上的两点,延长AM于点C,AB平分∠DAC,直线DB平分∠FBC,若∠ACB=100°,则∠DBA的度数为________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我市某重点中学校团委、学生会发出倡议,在初中各年级捐款购买书籍送给我市贫困地区的学校.初一年级利用捐款买甲、乙两种自然科学书籍若干本,用去5324元;初二年级买了A、B两种文学书籍若干本,用去4840元,其中A、B的数量分别与甲、乙的数量相等,且甲种书与B种书的单价相同,乙种书与A种书的单价相同.若甲、乙两种书的单价之和为121元,则初一和初二两个年级共向贫困地区的学校捐献了________本书.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小明一家利用国庆八天驾车到某景点旅游,小汽车出发前油箱有油35L,行驶若干小时后,途中在加油站加油若干升,油箱中余油量Q(L)与行驶时间t(h)之间的关系如图所示,根据图像回答下列问题:
(1)小汽车行驶______h后加油,中途加油_______L
(2)求加油前油箱余油量Q与行驶时间t的函数关系式
(3)如果小汽车在行驶过程中耗油量速度不变,加油站距景点200km,车速80km/h,要到达目的地,油箱中的油是否够用?请说明理由

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】公元前5世纪,毕达哥拉斯学派中的一名成员希伯索斯发现了无理数 ![]() ,导致了第一次数学危机,
,导致了第一次数学危机, ![]() 是无理数的证明如下: 假设
是无理数的证明如下: 假设 ![]() 是有理数,那么它可以表示成
是有理数,那么它可以表示成 ![]() (p与q是互质的两个正整数).于是(
(p与q是互质的两个正整数).于是( ![]() )2=(
)2=( ![]() )2=2,所以,q2=2p2 . 于是q2是偶数,进而q是偶数,从而可设q=2m,所以(2m)2=2p2 , p2=2m2 , 于是可得p也是偶数.这与“p与q是互质的两个正整数”矛盾.从而可知“
)2=2,所以,q2=2p2 . 于是q2是偶数,进而q是偶数,从而可设q=2m,所以(2m)2=2p2 , p2=2m2 , 于是可得p也是偶数.这与“p与q是互质的两个正整数”矛盾.从而可知“ ![]() 是有理数”的假设不成立,所以,
是有理数”的假设不成立,所以, ![]() 是无理数.
是无理数.
这种证明“ ![]() 是无理数”的方法是( )
是无理数”的方法是( )
A.综合法
B.反证法
C.举反例法
D.数学归纳法
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,∠BAC的平分线交△ABC的外接圆于点D,∠ABC的平分线交AD于点E, 
(1)求证:DE=DB;
(2)若∠BAC=90°,BD=4,求△ABC外接圆的半径.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某公司到果园基地购买某种优质水果,慰问医务工作者,果园基地对购买量在3000千克以上(含3000千克)的有两种销售方案,甲方案:每千克9元,由基地送货上门.乙方案:每千克8元,由顾客自己租车运回,已知该公司租车从基地到公司的运输费为5000元.
(1)分别写出该公司两种购买方案的付款y(元)与所购买的水果质量x(千克)之间的函数关系式,并写出自变量x的取值范围.
(2)依据购买量判断,选择哪种购买方案付款最少?并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点C,E,F,B在同一直线上,点A,D在BC异侧,AB∥CD,AE=DF,∠A=∠D.
(1)求证:AB=CD;
(2)若AB=CF,∠B=40°,求∠D的度数.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某件商品的成本价为15元,据市场调查得知,每天的销量y(件)与价格x(元)有下列关系:
销售价格x | 20 | 25 | 30 | 50 |
销售量y | 15 | 12 | 10 | 6 |
(1)根据表中数据,在直角坐标系中描出实数对(x,y)的对应点,并画出图象;
(2)猜测确定y与x间的关系式;
(3)设总利润为W元,试求出W与x之间的函数关系式,若售价不超过30元,求出当日的销售单价定为多少时,才能获得最大利润?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com