
����Ŀ��ij��˾�������ع���ij������ˮ����ο��ҽ�����ߣ������ضԹ�������3000ǧ�����ϣ���3000ǧ�ˣ������������۷�����������ÿǧ��9Ԫ���ɻ����ͻ����ţ��ҷ�����ÿǧ��8Ԫ���ɹ˿��Լ���˻أ���֪�ù�˾��ӻ��ص���˾�������Ϊ5000Ԫ��
(1)�ֱ�д���ù�˾���ֹ����ĸ���y��Ԫ�����������ˮ������x��ǧ�ˣ�֮��ĺ�����ϵʽ����д���Ա���x��ȡֵ��Χ��
(2)���ݹ������жϣ�ѡ�����ֹ����������٣���˵�����ɣ�
���𰸡���1������������2��������.
��������
����(1)�����ĸ���=��ˮ�����������������ҷ����ĸ���=��ˮ��������������+����ѣ�������������ϵ�ֱ���ʽ���ɣ�(2)�����ҵ����ַ�������ĸ��������бȽϣ��Ӷ�ȷ���������ķ�Χ.
�⣺(1)y��=9x(x��3000)��y��=8x+5000(x��3000)��
(2)��y��=y��ʱ����9x=8x+5000�����x=5000���൱x=5000ǧ��ʱ�����ָ���һ����
��y����y��ʱ����![]() �����3000��x��5000���൱3000��x��5000ʱ��ѡ����ַ��������٣�
�����3000��x��5000���൱3000��x��5000ʱ��ѡ����ַ��������٣�
��y�ף�y��ʱ����x��5000���൱x��5000ǧ��ʱ��ѡ�����ַ��������٣�
������������������С��5000ǧ��ʱ��ѡ�ü��������٣��ڹ���������5000ǧ��ʱ�����ַ�����ͬ���ڹ���������5000ǧ��ʱ��ѡ���ҷ���������.


 ���ſ����ϵ�д�
���ſ����ϵ�д� ���Ŀ����ϵ�д�
���Ŀ����ϵ�д� ������ӱ������ͯ������ϵ�д�
������ӱ������ͯ������ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ���ڵ���Rt��ABC�У���ACB=90����DΪBC���е㣬DE��AB������ΪE������B��BF��AC��DE���ӳ����ڵ�F������CF��

��1����֤��AD��CF��
��2������AF�����ж���ACF����״����˵�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��ABΪ��O��ֱ����BF�С�O�ڵ�B��AF����O�ڵ�D����C��DF�ϣ�BC����O�ڵ�E���ҡ�BAF=2��CBF��CG��BF�ڵ�G������AE�� 
��1��ֱ��д��AE��BC��λ�ù�ϵ��
��2����֤����BCG�ס�ACE��
��3������F=60�㣬GF=1�����O�İ뾶����
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ�٣��ھ���ABCD�У�AB��10 cm��BC��8 cm.��P�ӵ�A��������A��B��C��D��·���˶�������Dֹͣ����Q�ӵ�D��������D��C��B��A��·���˶�������Aֹͣ������P����Qͬʱ��������P���ٶ�Ϊÿ��1 cm����Q���ٶ�Ϊÿ��2 cm��a��ʱ����P����Qͬʱ�ı��ٶȣ���P���ٶȱ�Ϊÿ��b cm����Q���ٶȱ�Ϊÿ��d cm.ͼ���ǵ�P����x�����APD�����S1(cm2)��ʱ��x(��)�ĺ�����ϵͼ��ͼ���ǵ�Q����x�����AQD�����S2(cm2)��ʱ��x(��)�ĺ�����ϵͼ����
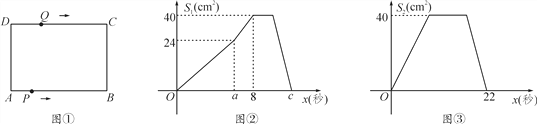
(1)����ͼ�ڣ���a�� b��ͼ����c��ֵ��
(2)��d��ֵ��
(3)���P�뿪��A��·��Ϊy1(cm)����Q����A����Ҫ�ߵ�·��Ϊy2(cm)����ֱ�д���ı��ٶȺ�y1��y2���������˶�ʱ��x(��)�ĺ�����ϵʽ���������P����Q����ʱx��ֵ��
(4)����Q����__ __��ʱ����Q���˶�·��Ϊ25 cm.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
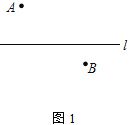
����Ŀ��(1) ��ͼ1����һ����ֱ�Ĺ�·���࣬�ֱ���A��B������ׯ������Ҫ�ڹ�·l�Խ�һ���������糧����A��B������ׯ���磬Ϊʹ���õĵ�����̣����ʹ��糧PӦ���ںδ�������ͼ��,��д������������ͼ�ۼ�;
(2) ��ͼ2����Ҫ��4����ׯA��B��C��D���磬���糧P�ָý��ںδ���ʹ���õ�������أ�����ͼ��,��д������������ͼ�ۼ���
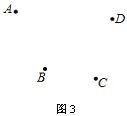
(3)A��B��C��D��ͼ3������AC���ӳ���E��ʹCE=AC������BD�������ӳ���F����д������������ͼ�ۼ�.
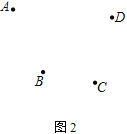
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����ͼ��B��C������߶�AD�ֳ�2��5��3�����֣�MΪAD���е㣬BM=6cm����CM��AD�ij���
![]()
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
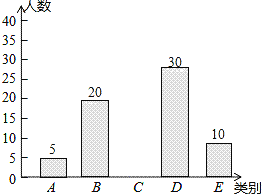
����Ŀ���ǽ�����ʱ��������Ż��⣬��������������Զ���ǽ�����һ����Ҫ��ʽ��Ϊ�˽�ijУ���꼶ѧ��ÿ���������������ʱ��������������������100������ѧ�������ݵ������õ���ͼ��ʾ��ͳ��ͼ����
��� | ʱ��t��Сʱ�� | ���� |
A | t��0.5 | 5 |
B | 0.5��t��1 | 20 |
C | 1��t��1.5 | a |
D | 1.5��t��2 | 30 |
E | t��2 | 10 |
�����ͼ����Ϣ����������⣺
��1��a=�� ����
��2����ȫ����ͳ��ͼ��
��3��С��˵������ÿ��Ķ���ʱ���ǵ����������ݵ���λ��������С��ÿ���������������ʱ����ʲô��Χ�ڣ�
��4������ÿ���������������ʱ����1Сʱ���϶�Ϊ������꣬���ѧ���Ĵ�����Ƕ��٣�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��������y=��x2+6x��x�ύ�ڵ�O��A������ΪB������E�������߶Գ����ϣ���F�ڶԳ����Ҳ��������ϣ���C��x���������ϣ���EF ![]()
![]() OC������OE��CF���ı���OCFE��
OC������OE��CF���ı���OCFE��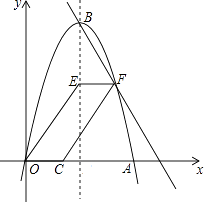
��1����B�����ꣻ
��2����tan��EOC= ![]() ʱ����Ȼ�����������ı����������������Ӧ�ĵ�F�����ꣻ
ʱ����Ȼ�����������ı����������������Ӧ�ĵ�F�����ꣻ
��3����0��tan��EOC��3ʱ������ÿһ��ȷ����tan��EOCֵ�������������ı���OCFE�����������������ı��ε����֮��Ϊ1��2ʱ����tan��EOC��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ���ڡ�ABC������C=90�㣬ADƽ�֡�BAC��DE��AB��E�������н���:��ADƽ�֡�CDE���ڡ�BAC=��BDE����DEƽ�֡�ADB����BE+AC=AB.������ȷ����( )
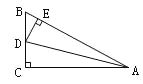
A. 1�� B. 2�� C. 3�� D. 4��
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com