
【题目】如图,在等腰Rt△ABC中,∠ACB=90°,D为BC的中点,DE⊥AB,垂足为E,过点B作BF∥AC交DE的延长线于点F,连接CF.

(1)求证:AD⊥CF;
(2)连接AF,试判断△ACF的形状,并说明理由.
【答案】(1)见解析;(2)△ACF是等腰三角形.见解析
【解析】
试题分析:(1)欲求证AD⊥CF,先证明∠CAG+∠ACG=90°,需证明∠CAG=∠BCF,利用三角形全等,易证.
(2)要判断△ACF的形状,看其边有无关系.根据(1)的推导,易证CF=AF,从而判断其形状.
(1)证明:在等腰直角三角形ABC中,
∵∠ACB=90°,
∴∠CBA=∠CAB=45°.
又∵DE⊥AB,
∴∠DEB=90°.
∴∠BDE=45°.
又∵BF∥AC,
∴∠CBF=90°.
∴∠BFD=45°=∠BDE.
∴BF=DB.
又∵D为BC的中点,
∴CD=DB.
即BF=CD.
在△CBF和△ACD中,
 ,
,
∴△CBF≌△ACD(SAS).
∴∠BCF=∠CAD.
又∵∠BCF+∠GCA=90°,
∴∠CAD+∠GCA=90°.
即AD⊥CF.
(2)△ACF是等腰三角形,理由为:
连接AF,如图所示,

由(1)知:△CBF≌△ACD,∴CF=AD,
∵△DBF是等腰直角三角形,且BE是∠DBF的平分线,
∴BE垂直平分DF,
∴AF=AD,
∵CF=AD,
∴CF=AF,
∴△ACF是等腰三角形.


 互动英语系列答案
互动英语系列答案科目:初中数学 来源: 题型:
【题目】如图,在直角坐标系中,点A(0,4),B(﹣3,4),C(﹣6,0),动点P从点A出发以1个单位/秒的速度在y轴上向下运动,动点Q同时从点C出发以2个单位/秒的速度在x轴上向右运动,过点P作PD⊥y轴,交OB于D,连接DQ.当点P与点O重合时,两动点均停止运动.设运动的时间为t秒.
(1)当t=1时,求线段DP的长;
(2)连接CD,设△CDQ的面积为S,求S关于t的函数解析式,并求出S的最大值;
(3)运动过程中是否存在某一时刻,使△ODQ与△ABC相似?若存在,请求出所有满足要求的t的值;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠ABC=90°,AB=8,BC=6.若DE是△ABC的中位线,延长DE交△ABC的外角∠ACM的平分线于点F,则线段DF的长为( )
A.7
B.8
C.9
D.10
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我们可以将任意三位数表示为![]() (其中a、b、c 分别表示百位上的数字,十位上的数字和个位上的数字,且a
(其中a、b、c 分别表示百位上的数字,十位上的数字和个位上的数字,且a![]() 0)显然,
0)显然,![]() = 100a+10b+c;我们把形如
= 100a+10b+c;我们把形如![]() 和
和![]() 的两个三位数称为一对“姊妹数”(其中x、y、z是三个连续的自然数)如:123和321是一对“姊妹数”,789和987是一对“姊妹数”.
的两个三位数称为一对“姊妹数”(其中x、y、z是三个连续的自然数)如:123和321是一对“姊妹数”,789和987是一对“姊妹数”.
(1)一对“姊妹数”的和为1110,求这对“姊妹数”.
(2)如果用x表示百位数字,试说明:任意一对“姊妹数”的和能被37整除.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,I是△ABC的内心,AI的延长线和△ABC的外接圆相交于点D,连接BI、BD、DC.下列说法中错误的一项是( ) 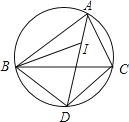
A.线段DB绕点D顺时针旋转一定能与线段DC重合
B.线段DB绕点D顺时针旋转一定能与线段DI重合
C.∠CAD绕点A顺时针旋转一定能与∠DAB重合
D.线段ID绕点I顺时针旋转一定能与线段IB重合
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知点A(a,0)和B(0,b)满足![]() ,分别过点A、B作x轴、y轴的垂线交于点C,如图,点P从原点出发,以每秒2个单位长度的速度沿着O-B-C-A-O的路线移动.
,分别过点A、B作x轴、y轴的垂线交于点C,如图,点P从原点出发,以每秒2个单位长度的速度沿着O-B-C-A-O的路线移动.
(1)写出A、B、C三点的坐标;
(2)当点P移动了6秒时,描出此时P点的位置,并写出点P的位置坐标;
(3)连结(2)中B、P两点,将线段BP向下平移h个单位(h>0),得到B′P′,若B′P′将四边形OACB的周长分成相等的两部分,求h的值.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知,在平面直角坐标系中,A(﹣3,﹣4),B(0,﹣2).

(1)△OAB绕O点旋转180°得到△OA1B1,请画出△OA1B1,并写出A1,B1的坐标;
(2)判断以A,B,A1,B1为顶点的四边形的形状,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某公司到果园基地购买某种优质水果,慰问医务工作者,果园基地对购买量在3000千克以上(含3000千克)的有两种销售方案,甲方案:每千克9元,由基地送货上门.乙方案:每千克8元,由顾客自己租车运回,已知该公司租车从基地到公司的运输费为5000元.
(1)分别写出该公司两种购买方案的付款y(元)与所购买的水果质量x(千克)之间的函数关系式,并写出自变量x的取值范围.
(2)依据购买量判断,选择哪种购买方案付款最少?并说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com